
V továrni na výrobu keramických dlaždíc je 5 % vyrobených dlaždíc chybných. Počas kontroly kvality výrobkov sa nájde iba 40 % chybných dlaždíc. Zvyšné dlaždice sú odoslané na predaj. Nájdite pravdepodobnosť, že náhodne vybraná dlaždica počas nákupu nebude mať chyby. Svoju odpoveď zaokrúhlite na stotiny.
Zobraziť riešeniePri kontrole kvality výrobkov sa zistí 40 % chybných dlaždíc, ktoré tvoria 5 % vyrobených dlaždíc a nie sú uvedené do predaja. To znamená, že 0,4 5 % = 2 % vyrobených obkladačiek nejde do predaja. Zvyšok vyrobených dlaždíc - 100% - 2% = 98% ide do predaja.
Bez chýb 100% - 95% vyrobených dlaždíc. Pravdepodobnosť, že zakúpená dlaždica nemá žiadnu chybu, je 95 % : 98 % = \frac(95)(98)\približne 0,97
Pravdepodobnosť, že batéria nie je nabitá, je 0,15. Zákazník si v obchode zakúpi náhodný balík, ktorý obsahuje dve tieto batérie. Nájdite pravdepodobnosť, že obe batérie v tomto balení sú nabité.
Zobraziť riešeniePravdepodobnosť nabitia batérie je 1-0,15 = 0,85. Nájdite pravdepodobnosť udalosti "obe batérie sú nabité". Označte A a B udalosti „prvý akumulátor je nabitý“ a „druhý akumulátor je nabitý“. Dostali sme P(A) = P(B) = 0,85. Udalosť „obe batérie sú nabité“ je priesečník udalostí A \ cap B, jej pravdepodobnosť sa rovná P(A\capB) = P(A)\cdot P(B) = 0,85\cdot 0,85 = 0,7225.
Zdroj: „Matematika. Príprava na skúšku-2017. úroveň profilu. Ed. F. F. Lysenko, S. Yu. Kulabukhova.
Pravdepodobnosť, že nová práčka bude opravená do roka, je 0,065. V istom meste sa za rok predalo 1200 práčok, z toho 72 kusov prešlo do záručnej dielne. Určte, nakoľko sa líši relatívna frekvencia výskytu udalosti „záručná oprava“ od jej pravdepodobnosti v tomto meste?
Zobraziť riešenieFrekvencia udalosti „práčka pôjde do záručnej opravy do roka“ sa rovná \frac(72)(1200) = 0,06. Od pravdepodobnosti sa líši o 0,065-0,06=0,005.
Zdroj: „Matematika. Príprava na skúšku-2017. úroveň profilu. Ed. F. F. Lysenko, S. Yu. Kulabukhova.
Pravdepodobnosť, že pero je chybné, je 0,05. Zákazník si v obchode kúpi náhodný balík, ktorý obsahuje dve perá. Nájdite pravdepodobnosť, že obe perá v tomto balení sú dobré.
Zobraziť riešeniePravdepodobnosť, že je pero v dobrom stave, je 1-0,05 = 0,95. Nájdite pravdepodobnosť udalosti „obe rukoväte fungujú“. Označte A a B udalosti „prvá rukoväť funguje“ a „druhá rukoväť funguje“. Dostali sme P(A) = P(B) = 0,95. Udalosť „obe rukoväte sú dobré“ je priesečník udalostí A \ cap B, jej pravdepodobnosť je rovná P(A\cap B) = P(A)\cdot P(B) = 0,95\cdot 0,95 = 0,9025.
Zdroj: „Matematika. Príprava na skúšku-2017. úroveň profilu. Ed. F. F. Lysenko, S. Yu. Kulabukhova.
Na obrázku je labyrint. Chrobák sa plazí do bludiska na mieste „Vchod“. Chrobák sa nemôže otočiť a plaziť opačným smerom, preto si na každom rozvetvení vyberie jednu z ciest, na ktorej ešte nebol. Aká je pravdepodobnosť, že chrobák príde k východu D, ak je výber ďalšej cesty náhodný.
Zobraziť riešenieUmiestnime šípky na križovatke v smeroch, ktorými sa môže chrobák pohybovať (pozri obr.).

Vyberme si na každej z križovatiek jeden smer z dvoch možných a budeme predpokladať, že keď narazí na križovatku, chrobák sa pohne smerom, ktorý sme si zvolili.
Aby sa chrobák dostal k východu D, treba na každej križovatke zvoliť smer označený plnou červenou čiarou. Celkovo sa výber smeru uskutoční 4-krát, vždy bez ohľadu na predchádzajúci výber. Pravdepodobnosť, že sa zakaždým vyberie plná červená šípka, je \frac12\cdot\frac12\cdot\frac12\cdot\frac12= 0,5^4= 0,0625.
Zdroj: „Matematika. Príprava na skúšku-2017. úroveň profilu. Ed. F. F. Lysenko, S. Yu. Kulabukhova.
V sekcii je 16 športovcov, medzi nimi dvaja priatelia - Olya a Masha. Športovci sú náhodne rozdelení do 4 rovnakých skupín. Nájdite pravdepodobnosť, že Olya a Masha sú v rovnakej skupine.

Začneme jednoduchými problémami a základnými pojmami teórie pravdepodobnosti.
Náhodný Udalosť sa nazýva udalosť, ktorú nemožno vopred presne predpovedať. Buď sa to môže stať, alebo nie.
Vyhrali ste v lotérii - náhodná udalosť. Pozvali ste priateľov na oslavu výhry a na ceste k vám sa zasekli vo výťahu – tiež náhodná udalosť. Je pravda, že majster bol nablízku a oslobodil celú spoločnosť za desať minút - a to možno považovať za šťastnú nehodu ...
Náš život je plný náhodných udalostí. O každom z nich sa dá povedať, že sa s niektorými stane pravdepodobnosť. S najväčšou pravdepodobnosťou tento koncept intuitívne poznáte. Teraz dáme matematickú definíciu pravdepodobnosti.
Začnime s najjednoduchším príkladom. Hádžete si mincou. Hlavy alebo chvosty?
Takáto akcia, ktorá môže viesť k jednému z niekoľkých výsledkov, sa v teórii pravdepodobnosti nazýva test.
Hlavy a chvosty - dve možné exodus testy.
Orol vypadne v jednom prípade z dvoch možných. To hovoria pravdepodobnosťže mince pristanú hlavy sa rovná .
Poďme si hodiť kockou. Kocka má šesť strán, takže existuje šesť možných výsledkov.
Tipovali ste napríklad, že tri body vypadnú. Toto je jeden výsledok zo šiestich možných. V teórii pravdepodobnosti bude tzv priaznivý výsledok.
Pravdepodobnosť získania trojnásobku je (jeden priaznivý výsledok zo šiestich možných).
Pravdepodobnosť štvorky je tiež
Ale pravdepodobnosť výskytu sedmičky je nulová. Na kocke totiž nie je tvár so siedmimi bodmi.
Pravdepodobnosť udalosti sa rovná pomeru počtu priaznivých výsledkov k celkovému počtu výsledkov.
Je zrejmé, že pravdepodobnosť nemôže byť väčšia ako jedna.
Tu je ďalší príklad. Vo vrecku jabĺk, z ktorých sú červené, ostatné sú zelené. Jablká sa nelíšia tvarom ani veľkosťou. Strčíš ruku do tašky a náhodne vyberieš jablko. Pravdepodobnosť nakreslenia červeného jablka je , a zeleného je .
Pravdepodobnosť získania červeného alebo zeleného jablka je .
Poďme analyzovať problémy v teórii pravdepodobnosti zahrnuté v zbierkach na prípravu na skúšku.
Taxi spoločnosť momentálne nemá autá: červené, žlté a zelené. Na zavolanie odišlo jedno z áut, ktoré bolo náhodou najbližšie k zákazníkovi. Nájdite pravdepodobnosť, že príde žltý taxík.
Celkovo je áut, teda jedno z pätnástich príde k zákazníkovi. Žltých je deväť, čo znamená, že pravdepodobnosť príchodu žltého auta je , teda .
V zbierke lístkov na biológiu všetkých lístkov, v dvoch z nich je otázka na huby. Na skúške študent dostane jeden náhodne vybraný tiket. Nájdite pravdepodobnosť, že tento tiket neobsahuje otázku o hubách.
Je zrejmé, že pravdepodobnosť vyžrebovania tiketu bez opýtania sa na huby je , teda .
Rodičovský výbor zakúpil na konci školského roka deťom ako darčeky skladačky, medzi ktorými boli obrazy známych umelcov a obrázky zvieratiek. Darčeky sa rozdávajú náhodne. Nájdite pravdepodobnosť, že Vovochka dostane zvieraciu hádanku.
Úloha sa rieši podobným spôsobom.
Odpoveď: .
Športovci sa zúčastňujú majstrovstiev v gymnastike: z Ruska, z USA, zvyšok - z Číny. Poradie, v ktorom gymnastky vystúpia, je určené žrebom. Nájdite pravdepodobnosť, že posledný súťažiaci športovec je z Číny.
Predstavme si, že všetci športovci v rovnakom čase pristúpili k klobúku a vytiahli z neho papieriky s číslami. Niektorí z nich dostanú dvadsiate číslo. Pravdepodobnosť, že to vytiahne čínsky športovec, je rovnaká (keďže športovci sú z Číny). Odpoveď: .
Študent bol požiadaný, aby pomenoval číslo od do . Aká je pravdepodobnosť, že pomenuje číslo, ktoré je násobkom piatich?
Každý piatyčíslo z danej množiny je deliteľné . Takže pravdepodobnosť je.
Hodí sa kocka. Nájdite pravdepodobnosť získania nepárneho počtu bodov.
Nepárne čísla; - dokonca. Pravdepodobnosť nepárneho počtu bodov je .
Odpoveď: .
Minca sa hodí trikrát. Aká je pravdepodobnosť dvoch hláv a jedného chvosta?
Všimnite si, že problém môže byť formulovaný inak: hádžu sa tri mince súčasne. Rozhodnutie to neovplyvní.
Koľko si myslíte, že existuje možných výsledkov?
Hodíme si mincou. Táto akcia má dva možné výsledky: hlavy a chvosty
Dve mince – už štyri výsledky:
Tri mince? Presne tak, výsledky, keďže .
Dve hlavy a jeden chvost sa zdvihnú trikrát z ôsmich.
Odpoveď: .
V náhodnom experimente sa hádžu dve kocky. Nájdite pravdepodobnosť, že súčet klesne o body. Výsledok zaokrúhlite na stotiny.
Hoď prvou kockou – šesť výsledkov. A pre každý z nich je možných šesť ďalších - keď hodíme druhou kockou.
Zistili sme, že táto akcia – hod dvoma kockami – má celkom možné výsledky, keďže .
A teraz tie dobré správy:
Pravdepodobnosť získania ôsmich bodov je .
Strelec s pravdepodobnosťou zasiahne cieľ. Nájdite pravdepodobnosť, že zasiahne cieľ štyrikrát za sebou.
Ak je pravdepodobnosť zásahu rovnaká, potom pravdepodobnosť chýbania je . Argumentujeme rovnakým spôsobom ako v predchádzajúcom probléme. Pravdepodobnosť dvoch zásahov za sebou je . A pravdepodobnosť štyroch zásahov za sebou sa rovná .
Peťa mal vo vrecku rubľové mince a rubľové mince. Peťa bez toho, aby sa obzrel, presunul nejaké mince do iného vrecka. Nájdite pravdepodobnosť, že päťrubľové mince sú teraz v rôznych vreckách.
Vieme, že pravdepodobnosť udalosti sa rovná pomeru počtu priaznivých výsledkov k celkovému počtu výsledkov. Ale ako vypočítať všetky tieto výsledky?
Môžete samozrejme označiť päťrubľové mince číslami a desaťrubľové mince číslami - a potom spočítať, koľkými spôsobmi si môžete vybrať tri prvky zo sady.
Existuje však jednoduchšie riešenie:
Mince kódujeme číslami:, (tieto sú päťrubľové), (tieto sú desaťrubľové). Stav problému možno teraz formulovať takto:
Existuje šesť žetónov očíslovaných od do . Koľkými spôsobmi sa dajú rovnomerne rozdeliť medzi dve vrecká, aby žetóny s číslami neskončili spolu?
Zapíšme si, čo máme v prvom vrecku.
K tomu poskladáme všetky možné kombinácie zo sady . Sada troch žetónov bude trojmiestne číslo. Je zrejmé, že v našich podmienkach ide o rovnakú sadu tokenov. Aby nám nič neuniklo a neopakovalo sa, usporiadame zodpovedajúce trojciferné čísla vzostupne:
Všetko! Vyskúšali sme všetky možné kombinácie počnúc . Pokračujeme:
celkové možné výsledky.
Máme podmienku - žetóny s číslami a nemali by byť spolu. To znamená, že nám napríklad nevyhovuje kombinácia – to znamená, že žetóny a oba skončili nie v prvom, ale v druhom vrecku. Priaznivé výsledky pre nás sú tie, kde je buď len, alebo len . Tu sú:
134, 135, 136, 145, 146, 156, 234, 235, 236, 245, 246, 256 - celkovo priaznivé výsledky.
Potom je požadovaná pravdepodobnosť .
Pravdepodobnosť, že nová rýchlovarná kanvica vydrží viac ako rok, je 0,93. Pravdepodobnosť, že bude trvať viac ako dva roky, je 0,87. Nájdite pravdepodobnosť, že to bude trvať menej ako dva roky, ale viac ako rok.
Po roku práce sa kanvica môže buď pokaziť v druhom roku, alebo bezpečne slúžiť aj po 2 rokoch prevádzky.
Nech je pravdepodobnosť, že čajník vydržal viac ako rok.
- pravdepodobnosť, že sa zlomí v druhom roku, - pravdepodobnosť, že bude trvať viac ako dva roky. samozrejme,
Odpoveď: 0,06
Udalosti, ktoré sa v rámci danej úlohy navzájom vylučujú, sa nazývajú nekompatibilné. Výskyt jednej z nezlučiteľných udalostí vylučuje výskyt iných.
Súčet dvoch udalostí je termín, ktorý znamená, že buď prvá udalosť, alebo druhá, alebo obe udalosti nastali naraz.
Pravdepodobnosť súčtu nezlučiteľných udalostí sa rovná súčtu ich pravdepodobností.
V našej úlohe sú nezlučiteľné udalosti „kanvica sa pokazila v druhom roku prevádzky“ a „kanvica funguje viac ako dva roky“. Kanvica je buď rozbitá alebo je stále funkčná.
Na obrázku je labyrint. Pavúk sa plazí do bludiska na mieste „Vchod“. Pavúk sa nemôže otočiť a plaziť sa späť. Na každom rozvetvení si pavúk vyberá cestu, ktorá sa ešte nepreplazila. Vzhľadom na náhodný výber ďalšej cesty určite, s akou pravdepodobnosťou pavúk opustí východ A.
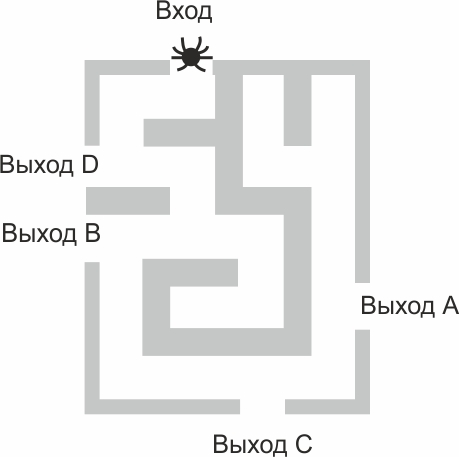
Očíslujeme vidlice, na ktorých sa pavúk môže náhodne otáčať jedným alebo druhým smerom.

Môže ísť buď k východu D a pravdepodobnosť tejto udalosti sa rovná Alebo ísť ďalej do labyrintu. Na druhej križovatke môže buď odbočiť do slepej uličky, alebo ísť k východu B (s pravdepodobnosťou, že na každej odbočke je pravdepodobnosť odbočenia jedným alebo druhým smerom rovná a keďže existuje päť odbočiek, pravdepodobnosť získania von cez východ A je 0,03125.
Udalosti A a B sa nazývajú nezávislé, ak pravdepodobnosť výskytu udalosti A nemení pravdepodobnosť výskytu udalosti B.
V našom probléme to platí: neinteligentný pavúk sa náhodne otočí doľava alebo doprava, bez ohľadu na to, čo urobil predtým.
Pre niekoľko nezávislých udalostí sa pravdepodobnosť, že nastanú všetky, rovná súčinu pravdepodobností.
(ALE) Dva kamióny, ktoré spolupracujú, odvážajú sneh z ulice Nizhnyaya Podgornaya a prvé nákladné auto musí absolvovať tri jazdy s nákladom snehu a druhé - dve. Pravdepodobnosť uviaznutia s nákladom snehu pri stúpaní je 0,2 pre prvý kamión a 0,25 pre druhý. Aká je pravdepodobnosť, že kamióny odpratávajú sneh z ulice Nižnaja Podgornaja bez toho, aby uviazli na kopci?
Pravdepodobnosť, že prvý kamión bezpečne prekoná kopec Pri druhom Keďže prvý kamión musí absolvovať 3 jazdy a druhý – dve, kamióny s pravdepodobnosťou nikdy neuviaznu na kopci
Poľnohospodárska firma nakupuje slepačie vajcia od dvoch domácností. 40% vajec z prvej farmy sú vajcia najvyššej kategórie a z druhej farmy - 20% vajec najvyššej kategórie. Celkovo 35 % vajec dostáva najvyššiu kategóriu. Nájdite pravdepodobnosť, že vajce zakúpené z tejto farmy bude z prvej farmy.
Nakreslite všetky možné výsledky situácie. Kupujúci prišiel do obchodu, ktorý patrí poľnohospodárskej firme, a kúpil vajíčko. Musíme nájsť pravdepodobnosť, že ide o vajce z prvej farmy.
Vajcia môžu byť len z prvej domácnosti, alebo z druhej a tieto dve udalosti sú nezlučiteľné. V tomto obchode nie sú žiadne iné vajcia.

Nech je pravdepodobnosť, že kúpené vajce z prvej farmy je . Potom je pravdepodobnosť, že vajce pochádza z druhej farmy (opačná udalosť), .
Vajcia môžu byť najvyššej kategórie a nie najvyššej.
V prvej farme je 40 % vajec najvyššej kategórie a 60 % nie je najvyššej kategórie. To znamená, že náhodne vybrané vajce z prvej farmy s pravdepodobnosťou 40% bude najvyššou kategóriou.
V druhej farme je 20 % vajec najvyššej kategórie a 80 % nie je najvyššej kategórie.
Nech je vajíčko náhodne vybrané v obchode z prvej farmy a najvyššej kategórie. Pravdepodobnosť tejto udalosti sa rovná súčinu pravdepodobností:
Pravdepodobnosť, že vajce z druhej farmy a najvyššej kategórie sa rovná
Ak tieto dve pravdepodobnosti spočítame, dostaneme pravdepodobnosť, že vajce má najvyššiu kategóriu. Podľa stavu má 35% vajec najvyššiu kategóriu, čo znamená, že táto pravdepodobnosť je 0,35.
Dostali sme rovnicu:
Vyriešime túto rovnicu a zistíme, že - pravdepodobnosť, že vajce zakúpené od tejto poľnohospodárskej spoločnosti sa ukázalo byť z prvej farmy.
Všetci pacienti s podozrením na hepatitídu robia krvný test. Ak test odhalí hepatitídu, potom sa výsledok testu nazýva pozitívny. U pacientov s hepatitídou poskytuje analýza pozitívny výsledok s pravdepodobnosťou 0,9. Ak pacient nemá hepatitídu, test môže poskytnúť falošne pozitívny výsledok s pravdepodobnosťou 0,01. Je známe, že 5 % pacientov prijatých s podozrením na hepatitídu má v skutočnosti hepatitídu. Nájdite pravdepodobnosť, že výsledok testu pacienta prijatého na kliniku s podozrením na hepatitídu bude pozitívny.
Čo priniesol pacient na kliniku? - Existuje podozrenie na hepatitídu. Možno je naozaj chorý na hepatitídu, alebo možno existuje iný dôvod jeho zlého zdravia. Možno len niečo zjedol. Pravdepodobnosť, že má hepatitídu, je 0,05 (t.j. 5 %). Pravdepodobnosť, že je zdravý, je 0,95 (t.j. 95 %).
Pacient je analyzovaný. Ukážme si na diagrame všetky možné výsledky:

Ak má hepatitídu, test dáva pozitívny výsledok s pravdepodobnosťou 0,9. To znamená, že analýza ukáže: "existuje hepatitída."
Upozorňujeme, že analýza neodhalí vo všetkých prípadoch hepatitídu u niekoho, kto je na ňu skutočne chorý. S pravdepodobnosťou 0,1 analýza nerozpozná u pacienta hepatitídu.
Ďalej. Test môže chybne poskytnúť pozitívny výsledok u niekoho, kto nemá hepatitídu. Pravdepodobnosť takéhoto falošne pozitívneho výsledku je 0,01. Potom, s pravdepodobnosťou 0,99, analýza poskytne negatívny výsledok, ak je osoba zdravá.
Nájdite pravdepodobnosť, že výsledok analýzy u pacienta prijatého na kliniku s podozrením na hepatitídu bude pozitívny.
Priaznivé výsledky pre túto situáciu: osoba je chorá a analýza je pozitívna (pravdepodobnosť súčasného výskytu týchto dvoch udalostí je ), alebo je osoba zdravá a analýza je falošne pozitívna (pravdepodobnosť súčasného výskytu týchto dvoch udalostí udalosti je ). Keďže udalosti „človek je chorý“ a „človek nie je chorý“ sú nezlučiteľné, pravdepodobnosť, že výsledok analýzy bude pozitívny, sa rovná
Odpoveď: 0,0545.
Na prijatie do ústavu pre odbor „lingvistika“ musí uchádzač Z. získať najmenej 70 bodov na Jednotnej štátnej skúške z každého z troch predmetov – matematiky, ruského jazyka a cudzieho jazyka. Ak sa chcete zapísať do špecializácie „Obchod“, musíte získať najmenej 70 bodov v každom z troch predmetov - matematika, ruský jazyk a spoločenské vedy.
Pravdepodobnosť, že uchádzač Z. získa aspoň 70 bodov z matematiky je 0,6, z ruštiny - 0,8, z cudzieho jazyka - 0,7 a zo spoločenských vied - 0,5.
Nájdite pravdepodobnosť, že Z. bude môcť zadať aspoň jednu z dvoch uvedených špecializácií.
Všimnite si, že problém sa nepýta, či uchádzač menom Z. bude študovať súčasne lingvistiku aj obchod a získa dva diplomy. Tu musíme nájsť pravdepodobnosť, že Z. bude môcť zadať aspoň jednu z týchto dvoch špecializácií - to znamená, že získa potrebný počet bodov.
Na zapísanie aspoň jednej z dvoch špecializácií musí Z. získať aspoň 70 bodov z matematiky. A v ruštine. A predsa – spoločenskovedné či zahraničné.
Pravdepodobnosť dosiahnutia 70 bodov z matematiky u neho je 0,6.
Pravdepodobnosť dosiahnutia bodov v matematike a ruštine je
Venujme sa cudzím a spoločenským štúdiám. Možnosti sú pre nás vhodné, keď uchádzač zabodoval v spoločenských štúdiách, v cudzom jazyku alebo v oboch. Možnosť nie je vhodná, ak nezískal body ani v jazyku, ani v „spoločnosti“. To znamená, že pravdepodobnosť úspešného absolvovania spoločenských štúdií alebo zahraničných štúdií aspoň na 70 bodov sa rovná
Výsledkom je, že pravdepodobnosť absolvovania matematiky, ruštiny a spoločenských vied alebo zahraničnej sa rovná Toto je odpoveď.
Pre úplné zvládnutie témy viď. Je to zadarmo.
Viac úloh USE na túto tému
Opakovanie kurzu teórie pravdepodobnosti v 11. ročníku. Príprava na skúšku.
Súčet udalostí A + B A AB nazývaná udalosť spočívajúca vo výskyte udalostiALE alebo udalostiIN , alebooboje tieto udalosti.
Príklad. Nechať byť ALE - prší, B - vtedy sneží (A+B) - buď dážď, alebo sneh, alebo dážď a sneh, teda zrážky;
ALE - ísť na diskotéku B - tak poďme do knižnice (A+B) - išiel buď na diskotéku alebo do knižnice, t.j. odišiel z domu.
Udalosti sú tzvnezlučiteľnéak výskyt jedného z nich vylučuje výskyt ostatných. To znamená, že môže nastať iba jedna konkrétna udalosť alebo iná.
Napríklad hodom kockou môžete rozlišovať medzi udalosťami, ako je párny počet bodov a nepárny počet bodov. Tieto udalosti sú nezlučiteľné.
Sčítací teorém pre pravdepodobnosti nezlučiteľných udalostí
Veta . Pravdepodobnosť výskytu jednej z dvoch nezlučiteľných udalostí, bez ohľadu na to, ktorá z nich, sa rovná súčtu pravdepodobností týchto udalostí:
P(A + B) = P(A) + P(B) .
Príklad. V urne je 30 loptičiek: 10 červených, 5 modrých a 15 bielych. Nájdite pravdepodobnosť, že sa objaví farebná guľa.
Riešenie . Vzhľad farebnej gule znamená vzhľad buď červenej alebo modrej gule.
Pravdepodobnosť výskytu červenej gule (udalosť A)
P(A) = 10/30 = 1/3.
Pravdepodobnosť modrej gule (udalosť B)
P (B) \u003d 5/30 \u003d 1/6.
Vývoj ALE A IN sú nekonzistentné (vzhľad gule jednej farby vylučuje vzhľad gule inej farby), preto platí veta o sčítaní.
Podľa vzorca požadovaná pravdepodobnosť
P(A + B) = P(A) + P(B) = 1/3 + 1/6 = 1/2 .
Príklad. Pravdepodobnosť získania 5 alebo 6 bodov na kocke v jednom hode bude 1/3 , pretože obe udalosti (pokles 5, pokles 6) sú nekompatibilné a pravdepodobnosť výskytu jednej alebo druhej udalosti sa vypočíta takto: 1/6 + 1/6 =1/3.
Kompletná skupina podujatí.
Súbor formulárov nekompatibilných udalostícelá skupina podujatí ak v dôsledku tohoindividuálny test jedna z týchto udalostí sa určite objaví.
Príklad. Pre kocky je typické zvážiť nasledujúcu množinu:
– v dôsledku hodu kockou vypadne 1 bod;
– … 2 body;
– … 3 body;
– … 4 body;
– … 5 bodov;
- ... 6 bodov.
Vývoj
![]() nezlučiteľné
(pretože vzhľad akejkoľvek tváre vylučuje súčasný vzhľad iných)
a vytvoriť kompletnú skupinu
(keďže jedna z týchto šiestich udalostí sa určite objaví ako výsledok testu)
.
nezlučiteľné
(pretože vzhľad akejkoľvek tváre vylučuje súčasný vzhľad iných)
a vytvoriť kompletnú skupinu
(keďže jedna z týchto šiestich udalostí sa určite objaví ako výsledok testu)
.
Veta . Súčet pravdepodobností udalostíA 1 , A 2 , …, A n , ktorý tvorí úplnú skupinu, sa rovná jednej:
P(A 1 ) + P(А 2 ) + ... + P(А n ) = 1 .
opačné udalosti.
Naproti pomenujte dve jedinečne možné udalosti, ktoré tvoria ucelenú skupinu. Ak je jedna z dvoch opačných udalostí označená akoALE , potom sa zvyčajne označuje druhý.
Príklad. Ak sa pri hode kockou event ALE spočíva v páde 6 , potom opačná udalosť je nepád 6 , t.j. vypadne 1, 2, 3, 4 alebo 5 .
Príklad. Ak ALE je teda párne číslo - nepárne číslo ak ALE - vtedy zima - nie zima (buď jeseň, leto, jar); ak ALE - zložil skúšku - neprešiel skúškou.
Veta. Súčet pravdepodobností opačných udalostí sa rovná jednej.
P(A) + P( ) = 1 aleboР(А) = 1 – Р( ).
Príklad. Aká je pravdepodobnosť, že pri hode dvoma kockami získajú rôzny (nie rovnaký) počet bodov?
Opísaný dej označte A. Opačný dej je dej , spočívajúci v tom, že na oboch kockách padol rovnaký počet bodov. udalosť šesť základných udalostí v prospech: (1;1), (2;2), (3;3), (4;4), (5;5), (6;6). Pravdepodobnosť každej z týchto elementárnych udalostí . Takže R( ) = . Potom Р(А) = 1 – Р( )= 1 - .
Závislé a nezávislé udalosti. Podmienená pravdepodobnosť.
Dve udalostiALE AIN volalnezávislý , ak pravdepodobnosť výskytu každého z nich nezávisí od toho, či nastala alebo nenastala iná udalosť.
Príklad. Minca sa hodí dvakrát. Udalosť A - "erb" vypadol pri prvom hode, udalosť B - "erb" vypadol pri druhom hode. Udalosti A a B sú nezávislé.
Udalosti A a B sa nazývajúzávislý ak pravdepodobnosť výskytu jednej z nich závisí od toho, či druhá udalosť nastala alebo nie.
Ak sa pravdepodobnosť udalosti B vypočíta za predpokladu, že udalosť A už nastala, potom sa táto pravdepodobnosť nazývapodmienená pravdepodobnosť udalosť B vo vzťahu k udalosti A. Označenie: P ALE (IN).
Príklad. Obálka obsahovala 4 pohľadnice s pohľadmi na Petrohrad a 3 pohľadnice s pohľadmi na Moskvu. Udalosťou A nech je vytiahnutie pohľadnice s výhľadmi na Petrohrad, udalosťou B vytiahnutím pohľadnice s pohľadmi na Moskvu. Zvážte pravdepodobnosti. spojené s týmito udalosťami.
a) ak najprv vytiahli pohľadnicu s výhľadom na Petrohrad a potom s výhľadom na Moskvu, tak P ALE (B) = ;
b) ak najprv vytiahli pohľadnicu s výhľadom na Moskvu a potom s výhľadom na Petrohrad, tak R. IN (A) = .
Súčin pravdepodobností.
Produkt dvoch udalostí A AIN zavolajte na udalosťAB , ktorá spočíva v spoločnom výskyte (kombinácii) týchto udalostí.
Príklad. Nechať byť ALE - z urny sa vytiahne biela guľa, B - potom sa z urny vytiahne biela guľa AB - vytiahnutý z urny dva biele gule; ak ALE - prší, B - sneží AB - dážď so snehom; ALE - párne číslo B - viacnásobné číslo 3 , potom AB - viacnásobné číslo 6 .
Veta o násobení pre nezávislé udalosti
Veta . Pravdepodobnosť súčinu dvoch nezávislých udalostíALE AIN sa rovná súčinu ich pravdepodobnosti:
P(AB) = P(A) P(B) .
Príklad. Kocka sa hodí dvakrát. Aká je pravdepodobnosť, že pri prvom hode padne 2 a pri druhom 6?
Nech udalosť A je 2-bodový hod, udalosť B je 6-bodový hod, udalosť C je 2-bodový hod pri prvom hode a 6 bodov pri druhom hode.
Udalosti A a B sú nezávislé, pretože výskyt jednej udalosti nezávisí od výskytu inej udalosti. Potom, keďže P(A) = a P(B) = potom P(C) = P(A) P(B) = .
Veta o násobení pre závislé udalosti.
Veta . Ak sú udalosti A a B závislé, potom sa pravdepodobnosť ich súčinu rovnásúčin pravdepodobnosti jedného z nich a podmienenej pravdepodobnosti druhého
P(AB) = P(A) P A (B) .
Príklad. Obálka obsahovala 4 pohľadnice s pohľadmi na Petrohrad a 3 pohľadnice s pohľadmi na Moskvu. Akcia A nech je po prvý raz vyťaženie pohľadov na Petrohrad, podujatie B po prvýkrát vytiahnutie pohľadov na Moskvu. Akcia C nech spočíva v tom, že najprv sa vytiahne pohľad na Petrohrad, potom pohľad na Moskvu. Potom sa udalosť C podľa definície násobenia rovná A·B. Je zrejmé, že v tomto prípade sú udalosti A a B závislé. Ukážme to.
Takže treba použiť vetu o vzorci na súčin závislých udalostí, t.j. P(C) = P(A)P A (B) . Teda P(C) = .
Príklad . Čitáreň má 6 učebnice informatiky, z toho tri viazaný. Knihovníčka vzala dva učebnica. Nájdite pravdepodobnosť, že oboje učebnice budú viazané.
Riešenie
. Zvážte nasledujúce udalosti:
ALE
1
- prvá prevzatá učebnica v obale;
A
2
- druhá prevzatá učebnica vo väzbe.
Udalosť A=A 1 A 2 , spočíva v tom, že obe prevzaté učebnice sú zviazané. Vývoj ALE 1 A ALE 2 sú závislé, pretože pravdepodobnosť výskytu udalosti ALE 2 závisí od výskytu udalosti ALE 1 . Preto na výpočet pravdepodobnosti používame vzorec produkty závislých udalostí .
Pravdepodobnosť udalosti ALE 1 podľa klasickej definície pravdepodobnosti:
P(A 1 a) = m/n = 3/6 = 0,5 .
P A1 (ALE 2 ) je definovaná ako podmienená pravdepodobnosť udalosti ALE 2 za predpokladu, že udalosť ALE 1 už dorazilo:
P A1 (ALE 2 ) = 2/5 = 0,4 .
Potom požadovaná pravdepodobnosť výskytu udalosti ALE :
P (A) \u003d 0,5 0,4 \u003d 0,2 .
Sčítací teorém pre pravdepodobnosti spoločných udalostí
Dve udalosti sa nazývajúkĺb , ak účasť jedného z nich nevylučuje účasť druhého v tom istom konaní.
Príklad. ALE - vzhľad štyroch bodov pri hode kockou; IN - výskyt párneho počtu bodov. Udalosť ALE A IN - kĺb.
Veta . Pravdepodobnosť výskytu aspoň jednej z dvoch spoločných udalostíALE AIN sa rovná súčtu pravdepodobností týchto udalostí bez pravdepodobnosti ich spoločného výskytu:
P(A + B) = P(A) + P(B) - P(AB) .
Príklad. Dvaja študenti čítajú knihu. Prvý študent dokončí knihu s pravdepodobnosťou 0,6; druhá je 0,8. Nájdite pravdepodobnosť, že knihu bude čítať aspoň jeden zo študentov.
Riešenie . Pravdepodobnosť, že knihu bude čítať každý zo študentov, nezávisí od výsledku jedného študenta, teda udalostí ALE (prvý študent dočítal knihu) a B (druhý študent dočítal knihu) sú samostatné a spolupracujú. Požadovanú pravdepodobnosť nájdeme pomocou vzorca na sčítanie pravdepodobnosti spoločných udalostí.
Pravdepodobnosť udalosti AB (obaja študenti dočítali knihu):
P(AB) = P(A) P(B) = 0,6 0,8 = 0,48.
Potom
P(A + B) = 0,6 + 0,8 - 0,48 = 0,92.
Príklad. Kávu v obchodnom centre predávajú dva rovnaké automaty. Pravdepodobnosť, že sa v automate do konca dňa minie káva, je 0,3. Pravdepodobnosť, že obom strojom dôjde káva, je 0,12. Nájdite pravdepodobnosť, že do konca dňa káva skončí aspoň v jednom z automatov (čiže buď v jednom, alebo v druhom, alebo v oboch naraz).
Pravdepodobnosť prvej udalosti „káva skončí v prvom automate“ ako aj pravdepodobnosť druhej udalosti „káva skončí v druhom automate“ podľa podmienky je rovná 0,3. Udalosti sú založené na spolupráci.
Pravdepodobnosť spoločnej realizácie prvých dvoch udalostí sa rovná 0,12 podľa podmienky.
To znamená, že pravdepodobnosť, že aspoň jednému z automatov dôjde do konca dňa káva, je 0,3 + 0,3 - 0,12 = 0,48.
Príklad. Škola má 1400 žiakov, z toho 1200 žiakov lyžuje, 952 žiakov vie korčuľovať. 60 žiakov nevie lyžovať ani korčuľovať. Aká je pravdepodobnosť, že študent vie lyžovať a korčuľovať?
Označte E - všetci žiaci tejto školy. Udalosťou A nech je schopnosť žiakov lyžovať. Podujatie B - schopnosť žiakov korčuľovať. Podujatie AB - schopnosť žiakov lyžovať a korčuľovať. Podujatie A + B - schopnosť žiakov lyžovať alebo korčuľovať. .
Vzorec úplnej pravdepodobnosti.
Ak udalosť A môže nastať len vtedy, ak sa vykoná jedna z udalostí B 1 , IN 2 , …, IN n ktoré tvoria ucelenú skupinu nezlučiteľných udalostí, potom sa pravdepodobnosť udalosti A vypočíta podľa vzorca
P(A) = P(B 1 ) · R V 1 (A) + P (B 2 ) · R V 2 (A) + ... + P (B n ) · R IN n (ALE).
Tento vzorec sa nazýva vzorec celkovej pravdepodobnosti. 3 ) = .
Nech je udalosť A, že vybraná lampa je chybná; R V 1 (ALE) znamená prípad, že sa zo žiaroviek vyrobených v prvom závode vyberie chybná žiarovka , P(B 2 ) - v druhom závode, Р(В 3 ) - v treťom závode. Zo stavu problému vyplýva:
R V 1 =0,034.

Bibliografia.
Tyurin Yu.N., Makarov A.A., Vysotsky I.R., Yashchenko I.V. Teória pravdepodobnosti a štatistika. JSC "Moskva učebnica". M., 2008.
Shakhmeister A.Kh. Kombinatorika. Štatistiky. Pravdepodobnosť. MTsNMO. M., 2010.
Doteraz prezentované v otvorenej banke USE problémov v matematike (mathege.ru), ktorých riešenie je založené iba na jednom vzorci, ktorý je klasickou definíciou pravdepodobnosti.
Najjednoduchší spôsob, ako pochopiť vzorec, sú príklady.
Príklad 1 V košíku je 9 červených loptičiek a 3 modré. Guličky sa líšia len farbou. Náhodne (bez pozerania) dostaneme jeden z nich. Aká je pravdepodobnosť, že takto vybraná lopta bude modrá?
Komentár. V problémoch v teórii pravdepodobnosti sa stane niečo (v tomto prípade naša akcia ťahania lopty), čo môže mať iný výsledok – výsledok. Treba poznamenať, že na výsledok sa dá pozerať rôznymi spôsobmi. "Vytiahli sme loptu" je tiež výsledkom. "Vytiahli sme modrú loptičku" je výsledok. „Vyžrebovali sme túto konkrétnu loptičku zo všetkých možných loptičiek“ – tento najmenej zovšeobecnený pohľad na výsledok sa nazýva elementárny výsledok. Vo vzorci na výpočet pravdepodobnosti sú myslené elementárne výsledky.
Riešenie. Teraz vypočítame pravdepodobnosť výberu modrej gule.
Udalosť A: „vybratá lopta bola modrá“
Celkový počet všetkých možných výsledkov: 9+3=12 (počet všetkých loptičiek, ktoré sme mohli vyžrebovať)
Počet priaznivých výsledkov pre udalosť A: 3 (počet takých výsledkov, pri ktorých došlo k udalosti A – teda počet modrých loptičiek)
P(A) = 3/12 = 1/4 = 0,25
Odpoveď: 0,25
Vypočítajme pre rovnaký problém pravdepodobnosť výberu červenej gule.
Celkový počet možných výsledkov zostane rovnaký, 12. Počet priaznivých výsledkov: 9. Požadovaná pravdepodobnosť: 9/12=3/4=0,75
Pravdepodobnosť akejkoľvek udalosti je vždy medzi 0 a 1.
Niekedy v bežnej reči (ale nie v teórii pravdepodobnosti!) Pravdepodobnosť udalostí sa odhaduje v percentách. Prechod medzi matematickým a konverzačným hodnotením sa robí násobením (alebo delením) 100 %.
takze
V tomto prípade je pravdepodobnosť nulová pre udalosti, ktoré sa nemôžu stať – nepravdepodobné. Napríklad v našom príklade by to bola pravdepodobnosť vytiahnutia zelenej lopty z koša. (Počet priaznivých výsledkov je 0, P(A)=0/12=0, ak sa počítajú podľa vzorca)
Pravdepodobnosť 1 má udalosti, ktoré sa úplne určite stanú, bez možností. Naším problémom je napríklad pravdepodobnosť, že „vybratá loptička bude buď červená alebo modrá“. (Počet priaznivých výsledkov: 12, P(A)=12/12=1)
Pozreli sme sa na klasický príklad, ktorý ilustruje definíciu pravdepodobnosti. Všetky podobné problémy USE v teórii pravdepodobnosti sa riešia pomocou tohto vzorca.
Namiesto červených a modrých loptičiek môžu byť jablká a hrušky, chlapci a dievčatá, naučené a nenaučené lístky, lístky obsahujúce a neobsahujúce otázku na určitú tému (prototypy , ), chybné a kvalitné tašky či záhradné čerpadlá (prototypy , ) - princíp zostáva rovnaký.
Mierne sa líšia vo formulácii úlohy teórie pravdepodobnosti USE, kde je potrebné vypočítať pravdepodobnosť udalosti nastávajúcej v určitý deň. ( , ) Rovnako ako v predchádzajúcich úlohách musíte určiť, čo je elementárny výsledok, a potom použiť rovnaký vzorec.
Príklad 2 Konferencia trvá tri dni. Prvý a druhý deň po 15 rečníkov, tretí deň 20. Aká je pravdepodobnosť, že správa profesora M. padne na tretí deň, ak sa poradie správ určí žrebom?
Aký je tu základný výsledok? - Priradenie posudku profesora k jednému zo všetkých možných sériových čísel prejavu. Do žrebovania sa zapojí 15+15+20=50 ľudí. Správa profesora M. tak môže dostať jedno z 50 čísel. To znamená, že existuje iba 50 základných výsledkov.
Aké sú priaznivé výsledky? - Tie, v ktorých sa ukáže, že profesor prehovorí na tretí deň. Teda posledných 20 čísel.
Podľa vzorca je pravdepodobnosť P(A)= 20/50=2/5=4/10=0,4
Odpoveď: 0,4
Žrebovanie je tu založenie náhodnej korešpondencie medzi ľuďmi a objednanými miestami. V príklade 2 sa porovnávanie posudzovalo z hľadiska toho, ktoré z miest môže konkrétna osoba zaujať. K rovnakej situácii môžete pristupovať aj z druhej strany: kto z ľudí by sa s akou pravdepodobnosťou mohol dostať na konkrétne miesto (prototypy , , , ):
Príklad 3 Na žrebovaní sa zúčastňuje 5 Nemcov, 8 Francúzov a 3 Estónci. Aká je pravdepodobnosť, že prvý (/druhý/siedmy/posledný - to je jedno) bude Francúz.
Počet elementárnych výsledkov je počet všetkých možných ľudí, ktorí by sa mohli dostať na dané miesto žrebom. 5+8+3=16 ľudí.
Priaznivé výsledky - Francúzi. 8 ľudí.
Požadovaná pravdepodobnosť: 8/16=1/2=0,5
Odpoveď: 0,5
Prototyp je mierne odlišný. Existujú úlohy o minciach () a kockách (), ktoré sú o niečo kreatívnejšie. Riešenia týchto problémov nájdete na stránkach prototypu.
Tu je niekoľko príkladov hodu mincou alebo kockou.
Príklad 4 Keď si hodíme mincou, aká je pravdepodobnosť, že dostaneme chvosty?
Výsledky 2 - hlavy alebo chvosty. (verí sa, že minca nikdy nepadne na hranu) Priaznivý výsledok - chvosty, 1.
Pravdepodobnosť 1/2=0,5
Odpoveď: 0,5.
Príklad 5Čo ak hodíme mincou dvakrát? Aká je pravdepodobnosť, že sa to v oboch prípadoch objaví?
Hlavná vec je určiť, ktoré základné výsledky budeme brať do úvahy pri hádzaní dvoch mincí. Po vhodení dvoch mincí môže nastať jeden z nasledujúcich výsledkov:
1) PP - v oboch prípadoch to skončilo na chvoste
2) PO - prvýkrát chvosty, druhýkrát hlavy
3) OP - prvý raz hlavy, druhý krát chvosty
4) OO - vedie v oboch prípadoch
Iné možnosti nie sú. To znamená, že existujú 4 základné výsledky. Len prvý je priaznivý, 1.
Pravdepodobnosť: 1/4 = 0,25
Odpoveď: 0,25
Aká je pravdepodobnosť, že dva hody mince dopadnú na chvosty?
Počet elementárnych výsledkov je rovnaký, 4. Priaznivé výsledky sú druhý a tretí, 2.
Pravdepodobnosť získania jedného chvosta: 2/4 = 0,5
Pri takýchto problémoch môže prísť vhod iný vzorec.
Ak pri jednom hode mincou máme 2 možné výsledky, potom pri dvoch hodoch bude 2 2=2 2 =4 (ako v príklade 5), pri troch hodoch 2 2 2=2 3 =8, pri štyroch : 2·2·2·2=2 4 =16, … pre N hodov možných výsledkov bude 2·2·...·2=2 N .
Môžete teda nájsť pravdepodobnosť získania 5 chvostov z 5 hodov mincou.
Celkový počet elementárnych výsledkov: 2 5 =32.
Priaznivé výsledky: 1. (RRRRRR - všetkých 5 krát chvosty)
Pravdepodobnosť: 1/32=0,03125
To isté platí pre kocky. Pri jednom hode je 6 možných výsledkov. Takže pri dvoch hodoch: 6 6=36, pri troch 6 6 6=216 atď.
Príklad 6 Hádžeme kockou. Aká je pravdepodobnosť získania párneho čísla?
Celkové výsledky: 6, podľa počtu tvárí.
Priaznivé: 3 výsledky. (2, 4, 6)
Pravdepodobnosť: 3/6 = 0,5
Príklad 7 Hoď dvoma kockami. Aká je pravdepodobnosť, že celkový počet hodí 10? (zaokrúhlené na stotiny)
Existuje 6 možných výsledkov pre jednu kocku. Pre dvoch je teda podľa vyššie uvedeného pravidla 6·6=36.
Aké výsledky budú priaznivé, ak celkovo 10 vypadne?
10 treba rozložiť na súčet dvoch čísel od 1 do 6. Dá sa to dvoma spôsobmi: 10=6+4 a 10=5+5. Takže pre kocky sú možné možnosti:
(6 na prvom a 4 na druhom)
(4 na prvom a 6 na druhom)
(5 na prvom a 5 na druhom)
Celkovo 3 možnosti. Požadovaná pravdepodobnosť: 3/36=1/12=0,08
Odpoveď: 0,08
O iných typoch problémov B6 sa bude diskutovať v jednom z nasledujúcich článkov „Ako ich vyriešiť“.
Pravdepodobnosť udalosti $A$ je pomer počtu výsledkov priaznivých pre $A$ k počtu všetkých rovnako možných výsledkov
$P(A)=(m)/(n)$, kde $n$ je celkový počet možných výsledkov a $m$ je počet výsledkov uprednostňujúcich $A$.
Pravdepodobnosť udalosti je číslo zo segmentu $$
Taxi spoločnosť má k dispozícii autá za 50 $. 35 $ z nich sú čierne, zvyšok je žltý. Nájdite pravdepodobnosť, že pri náhodnom zavolaní príde žlté auto.
Nájdite počet žltých áut:
Celkovo ide o autá za 50 $, teda jedno z päťdesiatich príde na zavolanie. Existuje 15 $ žltých áut, takže pravdepodobnosť príchodu žltého auta je $(15)/(50)=(3)/(10)=0,3 $
Odpoveď: 0,3 $
O dvoch udalostiach sa hovorí, že sú opačné, ak sú v danom pokuse nezlučiteľné a jedna z nich nevyhnutne nastane. Pravdepodobnosť opačných udalostí sa rovná 1. Udalosť opačná k udalosti $A$ sa zapíše $((A))↖(-)$.
$P(A)+P((A))↖(-)=1$
Dve udalosti $A$ a $B$ sa nazývajú nezávislé, ak pravdepodobnosť výskytu každej z nich nezávisí od toho, či druhá udalosť nastala alebo nie. V opačnom prípade sa udalosti nazývajú závislé.
Pravdepodobnosť súčinu dvoch nezávislých udalostí $A$ a $B$ sa rovná súčinu týchto pravdepodobností:
$P(A B)=P(A) P(B)$
Ivan Ivanovič si kúpil dva rôzne lístky do lotérie. Pravdepodobnosť, že prvý žreb vyhrá, je 0,15 USD. Pravdepodobnosť, že vyhrá druhý tiket lotérie, je 0,12 USD. Ivan Ivanovič sa zúčastňuje oboch žrebov. Za predpokladu, že žrebovanie prebieha nezávisle od seba, nájdite pravdepodobnosť, že Ivan Ivanovič vyhrá v oboch žreboch.
Pravdepodobnosť $P(A)$ - vyhrá prvý tiket.
Pravdepodobnosť $P(B)$ - vyhráva druhý tiket.
Udalosti $A$ a $B$ sú nezávislé udalosti. To znamená, že na nájdenie pravdepodobnosti, že nastanú obe udalosti, musíte nájsť súčin pravdepodobností
$P(A B)=P(A) P(B)$
$ P = 0,15 0,12 = 0,018 $
Odpoveď: 0,018 USD
Dve udalosti $A$ a $B$ sa považujú za nezlučiteľné, ak neexistujú žiadne výsledky v prospech udalosti $A$ aj udalosti $B$. (Udalosti, ktoré sa nemôžu stať súčasne)
Pravdepodobnosť súčtu dvoch nezlučiteľných udalostí $A$ a $B$ sa rovná súčtu pravdepodobností týchto udalostí:
$P(A+B)=P(A)+P(B)$
Na skúške z algebry dostane študent jednu otázku zo všetkých skúšok. Pravdepodobnosť, že ide o otázku týkajúcu sa kvadratických rovníc, je 0,3 $. Pravdepodobnosť, že ide o otázku týkajúcu sa iracionálnych rovníc, je 0,18 $. Neexistujú žiadne otázky týkajúce sa týchto dvoch tém súčasne. Nájdite pravdepodobnosť, že študent dostane na skúške otázku na jednu z týchto dvoch tém.
Tieto udalosti sa nazývajú nekompatibilné, pretože študent dostane otázku BUĎ na tému „Kvadrikulárne rovnice“, ALEBO na tému „Iracionálne rovnice“. Témy nie je možné zachytiť súčasne. Pravdepodobnosť súčtu dvoch nezlučiteľných udalostí $A$ a $B$ sa rovná súčtu pravdepodobností týchto udalostí:
$P(A+B)=P(A)+P(B)$
$ P \u003d 0,3 + 0,18 \u003d 0,48 $
Odpoveď: 0,48 $
Dve udalosti sa považujú za spoločné, ak výskyt jednej z nich nevylučuje výskyt druhej v tom istom pokuse. V opačnom prípade sa udalosti nazývajú nekompatibilné.
Pravdepodobnosť súčtu dvoch spoločných udalostí $A$ a $B$ sa rovná súčtu pravdepodobností týchto udalostí mínus pravdepodobnosť ich súčinu:
$P(A+B)=P(A)+P(B)-P(A B)$
Vo vestibule kina sú dva rovnaké kávovary. Pravdepodobnosť, že stroju do konca dňa dôjde káva, je 0,6 $. Pravdepodobnosť, že obom strojom dôjde káva, je 0,32 $. Nájdite pravdepodobnosť, že sa aspoň v jednom z automatov minie káva do konca dňa.
Označme udalosti, nech:
$A$ = káva skončí v prvom stroji,
$B$ = káva skončí v druhom prístroji.
$A B =$ káva sa minie v oboch automatoch,
$A + B =$ káva sa minie minimálne v jednom automate.
Podľa konvencie $P(A) = P(B) = 0,6; P(A B) = 0,32 USD.
Udalosti $A$ a $B$ sú spoločné, pravdepodobnosť súčtu dvoch spoločných udalostí sa rovná súčtu pravdepodobností týchto udalostí zníženému o pravdepodobnosť ich súčinu:
$P(A + B) = P(A) + P(B) − P(A B) = 0,6 + 0,6 − 0,32 = 0,88 $