
Je známe, že priebeh kvantovej mechaniky je jedným z najťažších na pochopenie. To nesúvisí ani tak s novým a „nezvyčajným“ matematickým aparátom, ako v prvom rade s ťažkosťami pochopenia z pohľadu klasickej fyziky revolučnými myšlienkami kvantovej mechaniky a zložitosťou interpretácie výsledkov.
Väčšina učebné pomôcky o kvantovej mechanike je prezentácia materiálu spravidla založená na analýze riešení stacionárnych Schrödingerových rovníc. Stacionárny prístup nám však neumožňuje priamo porovnávať výsledky riešenia kvantovomechanického problému s analogickými klasickými výsledkami. Okrem toho mnohé procesy študované v rámci kvantovej mechaniky (ako je prechod častice cez potenciálnu bariéru, rozpad kvázistacionárneho stavu atď.) sú v zásade nestacionárne, a preto môžu byť plne pochopené až na základe riešení nestacionárnej Schrödingerovej rovnice. Keďže počet analyticky vyriešených problémov je malý, použitie počítača v procese štúdia kvantovej mechaniky je obzvlášť dôležité.
Jednou zo základných rovníc kvantovej mechaniky je Schrödingerova rovnica, ktorá určuje zmenu stavov kvantových systémov v čase. Píše sa ako
kde H je hamiltonovský operátor systému, ktorý sa zhoduje s energetickým operátorom, ak nezávisí od času. Typ operátora je určený vlastnosťami systému. Pre nerelativistický pohyb častice hmoty v potenciálnom poli U (r) je operátor reálny a je reprezentovaný súčtom operátorov kinetickej a potenciálnej energie častice.
Ak sa častica pohybuje v elektromagnetickom poli, Hamiltonov operátor bude zložitý.
Hoci rovnica (1.1) je rovnicou prvého rádu v čase, vďaka prítomnosti imaginárnej jednotky má aj periodické riešenia. Preto sa Schrödingerova rovnica (1.1) často nazýva Schrödingerova vlnová rovnica a jej riešenie sa nazýva časovo závislá vlnová funkcia. Rovnica (1.1) pre známa forma operátor H vám umožňuje určiť hodnotu vlnovej funkcie v ktoromkoľvek nasledujúcom časovom okamihu, ak je táto hodnota v počiatočnom okamihu známa. Schrödingerova vlnová rovnica teda vyjadruje princíp kauzality v kvantovej mechanike.
Schrödingerovu vlnovú rovnicu možno získať na základe nasledujúcich formálnych úvah. V klasickej mechanike je známe, že ak je energia daná ako funkcia súradníc a hybnosti
potom prechod na klasickú Hamiltonovu - Jacobiho rovnicu pre akčnú funkciu S
možno získať z (1.3) formálnou transformáciou
Rovnica (1.1) sa získa rovnakým spôsobom z (1.3) pri prechode z (1.3) na operátorovú rovnicu formálnou transformáciou
ak (1.3) neobsahuje súčin súradníc a hybností, alebo obsahuje také súčiny z nich, ktoré po odovzdaní operátorom (1.4) medzi sebou pendlujú. Ak po tejto transformácii vyrovnáme výsledky pôsobenia na funkciu operátorov pravej a ľavej strany získanej operátorovej rovnosti, dostaneme sa k vlnovej rovnici (1.1). Tieto formálne transformácie by sme však nemali brať ako odvodenie Schrödingerovej rovnice. Schrödingerova rovnica je zovšeobecnením experimentálnych údajov. Nie je odvodený v kvantovej mechanike, rovnako ako nie sú odvodené Maxwellove rovnice v elektrodynamike a princíp najmenšej akcie (alebo Newtonove rovnice) v klasickej mechanike.
Je ľahké overiť, že rovnica (1.1) je splnená pre vlnovú funkciu
opisujúci voľný pohyb častice s určitou hodnotou hybnosti. Vo všeobecnom prípade je platnosť rovnice (1.1) dokázaná zhodou so skúsenosťami všetkých záverov získaných pomocou tejto rovnice.
Ukážme, že rovnica (1.1) implikuje dôležitú rovnosť
čo naznačuje, že normalizácia vlnovej funkcie je zachovaná v priebehu času. Vynásobme (1.1) vľavo funkciou *, rovnicu komplexne konjugovanú s (1.1) funkciou a odčítajme druhú od prvej získanej rovnice; potom nájdeme
Integráciou tohto vzťahu nad všetkými hodnotami premenných a zohľadnením samoväzbovosti operátora dostaneme (1.5).
Ak do vzťahu (1.6) dosadíme explicitný výraz pre Hamiltonov operátor (1.2) pre pohyb častice v potenciálnom poli, dostaneme Diferenciálnej rovnice(rovnica kontinuity)
kde je hustota pravdepodobnosti a vektor
možno nazvať vektorom hustoty prúdu pravdepodobnosti.
Komplexná vlnová funkcia môže byť vždy reprezentovaná ako
kde a sú skutočné funkcie času a súradníc. Teda hustota pravdepodobnosti
a hustota prúdu pravdepodobnosti
Z (1.9) vyplýva, že j = 0 pre všetky funkcie, pri ktorých funkcia Φ nezávisí od súradníc. Najmä j = 0 pre všetky reálne funkcie.
Riešenia Schrödingerovej rovnice (1.1) sú vo všeobecnosti znázornené komplexnými funkciami. Komplexné funkcie sú veľmi pohodlné, aj keď nie nevyhnutné. Namiesto jednej komplexnej funkcie môže byť stav systému opísaný dvoma reálnymi funkciami a splnením dvoch súvisiacich rovníc. Napríklad, ak je operátor H reálny, potom dosadením funkcie do (1.1) a oddelením reálnej a imaginárnej časti dostaneme systém dvoch rovníc
v tomto prípade má tvar hustota pravdepodobnosti a hustota prúdu pravdepodobnosti
Fourierova transformácia vlnovej funkcie charakterizuje rozdelenie hybnosti v kvantovom stave. Chcete sa stiahnuť integrálna rovnica s Fourierovou transformáciou potenciálu ako jadra.
Riešenie. Medzi funkciami a existujú dva vzájomne inverzné vzťahy.
Ak sa ako definícia použije vzťah (2.1) a aplikuje sa naň operácia, potom, berúc do úvahy definíciu 3-rozmernej funkcie,
ako výsledok, ako je ľahké overiť, dostaneme inverzný vzťah (2.2). Podobné úvahy sú použité nižšie pri odvodzovaní vzťahu (2.8).
potom pre Fourierovu transformáciu potenciálu, ktorý máme
Za predpokladu, že vlnová funkcia spĺňa Schrödingerovu rovnicu
Nahradením tu namiesto výrazov (2.1) a (2.3) dostaneme
V dvojitom integráli prechádzame od integrácie vzhľadom na premennú k integrácii vzhľadom na premennú a potom túto novú premennú opäť označíme. Integrál nad zmizne pre akúkoľvek hodnotu iba vtedy, ak je samotný integrand rovný nule, ale potom
Toto je požadovaná integrálna rovnica s Fourierovou transformáciou potenciálu ako jadra. Samozrejme, integrálnu rovnicu (2.6) možno získať len za podmienky, že existuje Fourierova transformácia potenciálu (2.4); na to musí napríklad potenciál klesať na veľké vzdialenosti, aspoň ako, kde.
Treba poznamenať, že z normalizačného stavu
nasleduje rovnosť
Dá sa to ukázať nahradením výrazu (2.1) za funkciu v (2.7):
Ak tu najprv vykonáme integráciu cez, potom môžeme ľahko získať vzťah (2.8).
kde je Hamiltonov operátor - analóg klasickej Hamiltonovej funkcie
![]()
kde a sú nahradené operátormi hybnosti x, y, z a súradnicami,,:
x → = x, y → = y, z → = z,
| (4.2) |
Schrödingerova rovnicaČasovo závislá Schrödingerova rovnica: kde je Hamiltonián systému. Separácia premenných. Píšeme Ψ (, t) = ψ () θ (t), kde ψ je funkcia súradníc a θ je funkcia času. Ak nezávisí od času, potom rovnica ψ = iћψ má tvar θψ = iћψθ resp. Ľavá strana je funkciou iba súradníc a pravá strana je nezávislá od premennej x. Preto sa obe strany poslednej rovnice musia rovnať rovnakej konštante, ktorú označíme E
teda θ (t) = exp (−iEt / ћ), ψ () = Eψ () a Ψ (, t) = ψ () exp (−iEt / ћ). Rovnica ψ () = Eψ () sa nazýva stacionárna Schrödingerova rovnica. Pre jednorozmerný systém s hmotnosťou m v poli s potenciálom U (x) má tvar:
Pre trojrozmerný systém s hmotnosťou m v poli s potenciálom U (): - (ћ 2 / 2 m) Δψ () + U () ψ () = Eψ (), kde Δ je Laplacián. |
Keďže Schrödingerova rovnica je lineárna rovnica najskôr v čase, potom s jeho pomocou pre danú hodnotu vlnovej funkcie Ψ (x, y, z, 0) v čase t = 0 nájdeme jej hodnotu v ľubovoľnom čase t - Ψ (x, y , z, t) ...
Schrödingerova rovnica pre stacionárny stav, keď potenciálna energia častice nezávisí od času, má tvar
| ψ () = Eψ (). | (4.3) |
Táto rovnica sa nazýva stacionárna Schrödingerova rovnica.
Keďže v stacionárnom stave
| Ψ (, t) = ψ () exp (−iEt / ћ) | (4.4) |
a pravdepodobnosť nájdenia častice v čase t v bode x, y, z je úmerná | Ψ (, t) |, potom je ~ | ψ (x, y, z) | 2, t.j. nezávisí od času. Podobne pravdepodobnosť detekcie hodnoty fyzikálnej veličiny charakterizujúcej systém sa tiež nemení s časom, pretože je vyjadrená ako štvorec modulu vlnovej funkcie.
Potenciálna energia U (x) v obdĺžnikovej studni spĺňa tieto podmienky:
Častica sa nachádza v oblasti 0 ≤ x ≤ L. Mimo tejto oblasti je ψ (x) = 0. Schrödingerova rovnica pre časticu v oblasti 0 ≤ x ≤ L
kde k = (2mE / ћ 2) 1/2. Z okrajových podmienok ψ (0) = 0, ψ (L) = 0 a podmienok spojitosti vlnovej funkcie vyplýva
Častica môže byť v jednom z mnohých diskrétnych stavov, ktoré má k dispozícii.
Každá hodnota energie E n zodpovedá vlnovej funkcii ψ n (x), ktorá pri zohľadnení podmienky normalizácie
![]()
má formu
|
|
(4.10) |
Na rozdiel od klasickej kvantovej častice v obdĺžnikovej studni nemôže mať energiu
E< ћ 2 π 2 /(2mL 2).
Состояния частицы ψ n в
одномерном поле бесконечной потенциальной ямы полностью описывается с помощью
одного квантового числа n. Спектр энергий дискретный.
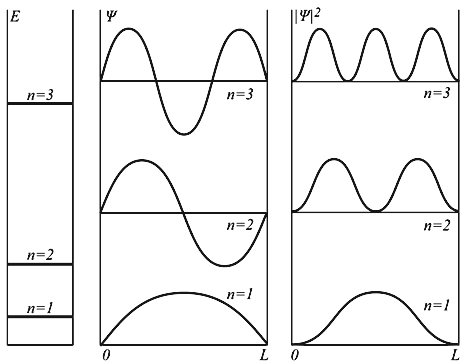
Ryža. 4.2. Energetické hladiny a vlnové funkcie častice Ψ v nekonečnej pravouhlej studni. Druhá mocnina modulu vlnovej funkcie | Ψ | 2 určuje pravdepodobnosť nájdenia častice v rôznych bodoch potenciálnej studne.
Poloha hladín častíc v potenciálovej studni závisí od typu potenciálovej studne. V jednorozmernej potenciálovej studni harmonického oscilátora má potenciálna energia tvar
Prípustné hodnoty celkovej energie sú určené vzorcom
| E n = ћω 0 (n + 1/2), n = 0, 1, 2, | (4.13) |
Na rozdiel od nekonečnej pravouhlej studne je spektrum úrovní harmonického oscilátora rovnako vzdialené.
S nárastom hmotnosti častice alebo veľkosti oblasti jej lokalizácie prechádza kvantový popis častice do klasického.
V sférických súradniciach má stacionárna Schrödingerova rovnica pre časticu v centrálnom potenciáli U (r) tvar
kde radiálna funkcia R nl (r) a uhlová funkcia Y lm (θ, φ), nazývaná sférická, spĺňajú rovnice
| 2 Y lm (θ, φ) = ћ 2 l(l+1) Y lm (θ, φ) | (4.16) |
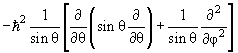 Y lm (θ, φ) = ћ 2 l(l+1) Y lm (θ, φ) Y lm (θ, φ) = ћ 2 l(l+1) Y lm (θ, φ) |
(4.17) |
Rovnica (4.16) určuje možné vlastné hodnoty l a vlastné funkcie Y lm (θ, φ) operátora s druhou mocninou momentu 2. Rovnica (4.17) určuje vlastné hodnoty energie E a radiálnych vlastných funkcií R nl (r), od ktorých závisí energia sústavy (obr. 4.3).
Úrovňový diagram (sekvencia a absolútne hodnoty energií) závisí od radiálnej funkcie R nl (r), ktorá je zase určená potenciálom U (r), v ktorom sa častica nachádza.
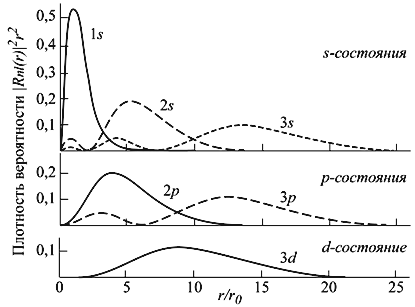
Ryža. 4.3. Radiálne rozdelenie pravdepodobnosti nájdenia elektrónu v Coulombovom poli protónu (atómu vodíka). Vzdialenosti sú uvedené v Bohrových polomeroch.
r0 = ћ 2 / m e e 2 ≈ 0,529 · 10 8 cm.
Vlastné hodnoty L 2 a L z sú riešením rovníc
2 Y lm (θ, φ) = L 2 Y lm (θ, φ) az Y lm (θ, φ) = L z Y lm (θ, φ).
Majú nasledujúce diskrétne hodnoty
L 2 = ћ 2 l (l + 1), kde l = 0, 1, 2, 3, ...,
L z = ћm, kde m = 0, ± 1, ± 2, ± 3,…, ± l.
Na charakterizáciu stavov s rôznymi hodnotami orbitálneho momentu hybnosti l sa zvyčajne používa nasledujúci zápis:
Spektroskopické názvy orbitálnych momentov l
| l = 0 | s-stav |
| l = 1 | p-stav |
| l = 2 | d-stav |
| l = 3 | f-stav |
| l = 4 | g-stav |
| l = 5 | h-stav |
| a atď. |
Stav s l = 0 zodpovedá sféricky symetrickej vlnovej funkcii. V prípadoch, keď l ≠ 0 vlnová funkcia nemá sférickú symetriu. Symetria vlnovej funkcie je určená symetriou sférických funkcií Y lm (θ, φ). Zaujímavý kvantový jav nastáva, keď riešenie sféricky symetrického problému (potenciál opisuje sféricky symetrický systém) vedie k stavom, ktoré sférickú symetriu nemajú. Symetria rovníc by sa teda nemala nevyhnutne odrážať v symetrii každého jednotlivého riešenia týchto rovníc, ale iba v súhrne tieto rozhodnutia.
Pre časticu so sféricky symetrickým potenciálom je hodnota orbitálneho momentu hybnosti L:
| (4.18) |
Zvyčajne, pre jednoduchosť, keď hovoríme o veľkosti orbitálneho momentu hybnosti, táto hodnota sa nazýva kvantové číslo l, čo znamená, že medzi l a L existuje vzťah jedna k jednej (4.18).
Pretože hodnota l môže nadobúdať iba celočíselné hodnoty 0, 1, 2, 3, ..., potom je orbitálny moment hybnosti L kvantovaný. Napríklad pre časticu s l = 2 moment hybnosti
=
= 6,58 · 10 -22 √6 MeV · sek. ≈ 2,6 · 10 - 34 J · sek.
Priestorové kvantovanie... Orbitálny moment hybnosti je vektorová veličina. Pretože veľkosť orbitálneho momentu hybnosti je kvantovaná, je kvantovaný aj smer vzhľadom na zvolený smer z, napríklad k vonkajšiemu magnetickému poľu, a nadobúda diskrétne hodnoty Lz = ћm, kde m sa mení od + l do –l, teda má 2l + 1 hodnoty. Napríklad pre l = 2 nadobúda hodnota m hodnoty +2, +1, 0, -1, -2 (pozri obr. 4.4). Zároveň energia systému nezávisí od m, teda od smeru vektora, čo je zrejmý dôsledok sférickej symetrie systému.
Stav častice v sféricky symetrickom poli je plne opísaný tromi kvantovými číslami: n, l a m.
Vzhľad kvantových čísel je spojený so symetrickými vlastnosťami systému. Povaha tejto symetrie určuje možné hodnoty kvantových čísel. Je zrejmé, že systém opísaný funkciou e im φ nadobudne predchádzajúcu hodnotu iba vtedy, keď azimutálny uhol φ v dôsledku rotácie okolo osi z nadobudne predchádzajúcu hodnotu φ. Funkcia e im φ túto podmienku spĺňa len v prípade, keď je veličina mφ násobkom 2π. Tie. hodnota m musí mať celočíselné hodnoty. Keďže je potrebné vziať do úvahy rotáciu v dvoch opačných smeroch a absenciu rotácie, jediné možné hodnoty sú m = 0, ± 1, ± 2,….
Spin je správny moment hybnosti častice. Vzťah medzi hodnotou vektora spinu a kvantovým počtom spinov s je rovnaký ako medzi hodnotou vektora orbitálneho momentu hybnosti a orbitálnym kvantovým číslom l:
| 2 = ћ 2 s (s + 1) | (4.19) |
Na rozdiel od orbitálneho kvantového čísla l, ktoré môže byť iba celé číslo alebo nula, spinové kvantové číslo s (ďalej len spin) môže byť buď celé číslo (vrátane nuly) alebo polovičné celé číslo, t.j. s = 0, 1/2, 1 , 3/2, 2, 5/2, ..., ale súčasne pre každý elementárna častica spin môže nadobudnúť jedinú hodnotu, ktorá je vlastná tomuto typu častíc... Takže spiny π-mezónov a K-mezónov sú rovné 0. Spiny elektrónu, protónu, neutrína, kvarkov a ich antičastíc sú rovné 1/2. Spin fotónu je 1. Bozóny sú triedou častíc s celočíselným spinom, zatiaľ čo spin fermiónov je polovičný. Spin častice sa nedá zmeniť, rovnako ako jej náboj či hmotnosť. Toto je jeho nemenná kvantová charakteristika.
Rovnako ako v prípade iných kvantových vektorov môže projekcia spinového vektora na ľubovoľný pevný smer v priestore (napríklad os z) nadobúdať hodnoty 2 s + 1:
s z ћ = ± sћ, ± (s - 1) ћ, ± (s - 2) ћ, ..., ± 1 / 2ћ alebo 0.
Číslo s z je kvantové číslo spinovej projekcie. Maximálna hodnota s z sa zhoduje s s. Keďže spin elektrónu je 1/2, priemet tohto spinu môže nadobudnúť iba dve hodnoty s z = ± 1/2. Ak je projekcia +1/2, potom hovoria, že rotácia je nahor, ak je projekcia -1/2, potom hovoria, že rotácia je dole.
Celkový moment hybnosti častice alebo systému častíc je vektorový súčet orbitálneho a spinového momentu hybnosti.
Na druhej mocnine celkového okamihu záleží:
2 = ћ 2 j (j + 1).
Kvantové číslo celkovej hybnosti j, zodpovedajúce súčtu dvoch vektorov a môže nadobudnúť množstvo diskrétnych hodnôt, ktoré sa líšia o 1:
j = l + s, l + s −1, ..., | l - s |
Projekcia na zvýraznenú os J z tiež nadobúda diskrétne hodnoty:
Jz = ћjz; = -j, -j + 1, ..., j - 1, j.
Počet hodnôt priemetu J z sa rovná 2j + 1. Ak sú určené pre a jediné hodnoty priemetov na osi z lz a sz, potom je jz tiež jednoznačne určené: jz = lz + s z.
Kvantové čísla sú celé čísla alebo zlomkové čísla, ktoré definujú všetky možné hodnoty fyzikálnej veličiny, ktorá charakterizuje rôzne kvantové systémy - atómy, atómové jadrá, kvarky a iné častice.
| n | Radiálne kvantové číslo. Určuje počet uzlov vlnovej funkcie a energiu systému. n = 1, 2,..., ∞. |
| J J | Celkový moment hybnosti J a jeho kvantové číslo j. Ten nie je nikdy negatívny a môže byť celý alebo polovičný v závislosti od vlastností posudzovaného systému. 2 = ћ 2 j (j + 1). |
| L, l | Orbitálny moment hybnosti L a jeho kvantové číslo l. Interpretácia l je rovnaká ako j, ale l môže nadobúdať iba celočíselné hodnoty vrátane nuly: l = 0, 1, 2,…. L2 = ћ 2 l (l + 1). |
| m | Magnetické kvantové číslo. Priemet celkového alebo orbitálneho momentu hybnosti na určenú os (zvyčajne os z) je mћ. Pre celkový moment m = ± j, ± (j-1),…, ± 1/2 alebo 0. Pre orbitál m = ± l, ± (l-1),…, ± 1, 0. |
| S, s | Spin uhlová hybnosť S a jeho kvantové číslo s. Môže to byť buď kladné celé číslo (vrátane nuly) alebo polovičné celé číslo. s - konštantná charakteristika častice určitého typu. S2 = ћ 2 s (s + 1). |
| s z | Kvantové číslo projekcie spinu hybnostičastice na zvýraznenej osi. Táto projekcia môže nadobudnúť hodnoty s z ћ, kde s z = ± s, ± (s -1),…, ± 1/2 alebo 0. |
| P alebo π | Priestorová parita. Charakterizuje správanie sa systému pri priestorovej inverzii → - (zrkadlový odraz). Celková parita častice je Р = π (-1) l, kde π je jej vnútorná parita a (-1) l je jej orbitálna parita. Vnútorné parity kvarkov sú kladné, antikvarky záporné. |
| ja | Isospin. Charakterizuje vlastnosť nemennosti náboja silných interakcií |
Písmeno J sa často používa na označenie spinového momentu.
Všetky stavy, v ktorých sa kvantový systém môže nachádzať, sú opísané pomocou kompletného súboru kvantových čísel. Takže v prípade protónu v jadre je stav protónu opísaný pomocou štyroch kvantových čísel zodpovedajúcich štyrom stupňom voľnosti – trom priestorovým súradniciam a spinu. Toto
Popísať sféricky symetrické systémy v kvantová fyzika používajú sa rôzne sféricky symetrické potenciály s rôznou radiálnou závislosťou:
![]()
kde U 0, a a R sú kladné konštanty (R je polomer jadra). Vo všetkých prípadoch možno sféricky symetrické systémy popísať pomocou množiny kvantových čísel n, l, j, j z, avšak v závislosti od radiálnej formy potenciálu bude energetické spektrum stavov systému rôzne.
Existencia fyzikálnych veličín zachovaných v čase úzko súvisí so symetrickými vlastnosťami hamiltoniánu systému. Napríklad, ak má kvantový systém stredovú symetriu U = U (r), potom tento systém zodpovedá zachovaniu orbitálneho momentu hybnosti l a jednej z jeho projekcií m. V tomto prípade, vzhľadom na sférickú symetriu problému, energia stavov nebude závisieť od hodnoty m, t.j. stavy budú degenerované v m.
Spolu s priestorovými symetriami spojenými s kontinuálnymi transformáciami existujú v kvantovej fyzike ďalšie diskrétne symetrie. Jednou z nich je zrkadlová symetria vlnovej funkcie vzhľadom na inverziu súradníc (→ -). Operátor inverzie zodpovedá kvantovému paritnému číslu, ktoré môže nadobudnúť dve hodnoty +1 a -1 v závislosti od toho, či sa znamienko vlnovej funkcie zachová počas inverzie alebo obrátenia.
Systém identických častíc sa vyznačuje ešte jednou symetriou - symetriou vzhľadom na permutácie identických častíc. Táto symetria je určená vlastnosťami častíc, ktoré tvoria systém. Systémy častíc s celočíselným spinom (bozóny) sú opísané symetrickými vlnovými funkciami, systémy častíc s polovičným spinom (fermióny) - antisymetrickými vlnovými funkciami.
1. Úvod
Kvantová teória sa zrodila v roku 1900, keď Max Planck navrhol teoretický záver o vzťahu medzi teplotou telesa a žiarením vyžarovaným týmto telesom – záver, že na dlhú dobu Podobne ako jeho predchodcovia Planck navrhol, že žiarenie vyžarujú atómové oscilátory, no zároveň veril, že energia oscilátorov (a teda aj žiarenie, ktoré vyžarujú) existuje vo forme malých diskrétnych častí, ktoré Einstein nazval kvantá. Energia každého kvanta je úmerná frekvencii žiarenia. Hoci vzorec odvodený Planckom vyvolal všeobecný obdiv, jeho predpoklady zostali nepochopiteľné, pretože odporovali klasickej fyzike.
V roku 1905 Einstein použil kvantovú teóriu na vysvetlenie niektorých aspektov fotoelektrického javu – emisie elektrónov z kovového povrchu, ktorý je vystavený ultrafialovému žiareniu. Počas cesty si Einstein všimol zjavný paradox: svetlo, o ktorom bolo dve storočia známe, že sa šíri ako súvislé vlny, sa za určitých okolností môže správať ako prúd častíc.
Asi o osem rokov neskôr Niels Bohr rozšíril kvantovú teóriu na atóm a vysvetlil frekvencie vĺn vyžarovaných atómami excitovanými plameňom alebo elektrickým nábojom. Ernest Rutherford ukázal, že hmotnosť atómu je takmer celá sústredená v centrálnom jadre, ktoré nesie kladný elektrický náboj a je v relatívne veľkých vzdialenostiach obklopené elektrónmi nesúcimi záporný náboj, v dôsledku čoho je atóm ako celok elektricky neutrálny. Bohr navrhol, že elektróny môžu byť iba na určitých diskrétnych dráhach zodpovedajúcich rôznym energetickým hladinám a že „skok“ elektrónu z jednej dráhy na druhú s nižšou energiou je sprevádzaný emisiou fotónu, ktorého energia sa rovná energetickému rozdielu medzi dvoma obežnými dráhami. Frekvencia je podľa Planckovej teórie úmerná energii fotónu. Bohrov model atómu teda vytvoril vzťah medzi rôznymi spektrálnymi čiarami charakteristickými pre látku emitujúcu žiarenie a štruktúrou atómu. Napriek počiatočnému úspechu si Bohrov model atómu čoskoro vyžiadal úpravy, aby sa odstránil rozpor medzi teóriou a experimentom. Navyše kvantová teória v tom štádiu ešte neposkytovala systematický postup na riešenie mnohých kvantových problémov.
Nová základná funkcia kvantová teória sa prejavilo v roku 1924, keď de Broglie predložil radikálnu hypotézu o vlnovej povahe hmoty: ak elektromagnetické vlny svetlo sa napríklad niekedy správa ako častice (ako to ukázal Einstein), častice, napríklad elektrón za určitých okolností, sa môžu správať ako vlny. V de Broglieho formulácii frekvencia zodpovedajúca častici súvisí s jej energiou, ako v prípade fotónu (častice svetla), ale matematický výraz navrhnutý de Brogliem bol ekvivalentný pomer medzi vlnovou dĺžkou a hmotnosťou. častica a jej rýchlosť (hybnosť). Existenciu elektronických vĺn experimentálne dokázali v roku 1927 Clinton Davisson a Lester Germer v USA a John-Paget Thomson v Anglicku.
Schrödinger, zaujatý Einsteinovými komentármi k de Broglieho myšlienkam, sa pokúsil aplikovať vlnový popis elektrónov na konštrukciu konzistentnej kvantovej teórie nesúvisiacej s Bohrovým neadekvátnym atómovým modelom. V istom zmysle zamýšľal priblížiť kvantovú teóriu klasickej fyzike, v ktorej sa nahromadilo mnoho príkladov matematického popisu vĺn. Prvý pokus Schrödingera v roku 1925 skončil neúspechom.
Rýchlosti elektrónov v Schrödingerovej teórii II boli blízke rýchlosti svetla, čo si vyžiadalo zahrnutie Einsteinovej špeciálnej teórie relativity do nej a zohľadnenie výrazného nárastu hmotnosti elektrónu pri veľmi vysokých rýchlostiach, ktoré predpovedala.
Jedným z dôvodov zlyhania Schrödingera bolo, že nezohľadnil prítomnosť špecifickej vlastnosti elektrónu, dnes známej ako spin (rotácia elektrónu okolo vlastnej osi ako vrchol), o ktorej sa hovorilo len málo. v tom čase známy.
Ďalší pokus urobil Schrödinger v roku 1926. Tentoraz zvolil rýchlosti elektrónov tak nízke, že potreba odvolávať sa na teóriu relativity sama od seba zmizla.
Druhý pokus bol korunovaný odvodením Schrödingerovej vlnovej rovnice, ktorá poskytuje matematický popis hmoty z hľadiska vlnovej funkcie. Schrödinger nazval svoju teóriu vlnová mechanika... Riešenia vlnovej rovnice boli v súlade s experimentálnymi pozorovaniami a mali hlboký vplyv na následný vývoj kvantovej teórie.
Krátko predtým publikovali Werner Heisenberg, Max Born a Pascual Jordan ďalšiu verziu kvantovej teórie nazvanú maticová mechanika, ktorá popisovala kvantové javy pomocou tabuliek pozorovateľných veličín. Tieto tabuľky predstavujú určitým spôsobom usporiadané matematické množiny, nazývané matice, nad ktorými možno podľa známych pravidiel vykonávať rôzne matematické operácie. Maticová mechanika tiež umožňovala súhlas s pozorovanými experimentálnymi údajmi, no na rozdiel od vlnovej mechaniky neobsahovala žiadne špecifické odkazy na priestorové súradnice alebo čas. Heisenberg obzvlášť trval na opustení akýchkoľvek jednoduchých vizuálnych reprezentácií alebo modelov v prospech iba tých vlastností, ktoré bolo možné určiť z experimentu.
Schrödinger ukázal, že vlnová mechanika a maticová mechanika sú matematicky ekvivalentné. Teraz súhrnne známe ako kvantová mechanika, tieto dve teórie poskytli dlho očakávaný spoločný základ pre popis kvantových javov. Mnohí fyzici uprednostňovali vlnovú mechaniku, pretože ich matematický aparát im bol viac známy a jeho koncepty sa zdali viac „fyzikálne“; operácie na maticách sú ťažkopádnejšie.
Funkcia Ψ. Normalizácia pravdepodobnosti.
Objav vlnových vlastností mikročastíc naznačil, že klasická mechanika nemôže poskytnúť správny popis správania takýchto častíc. Vznikla potreba vytvoriť mechaniku mikročastíc, ktorá by zohľadňovala aj ich vlnové vlastnosti. Nová mechanika vytvorená Schrödingerom, Heisenbergom, Diracom a ďalšími sa nazýva vlnová alebo kvantová mechanika.
Plane de Broglie vlna
(1)je veľmi špeciálna vlnová formácia zodpovedajúca voľnej rovnomerný pohybčastice v určitom smere a s určitou hybnosťou. Ale častica aj vo voľnom priestore a najmä v silových poliach môže vykonávať iné pohyby opísané zložitejšími vlnovými funkciami. V týchto prípadoch nie je úplný popis stavu častice v kvantovej mechanike daný rovinou de Broglieho vlny, ale nejakou zložitejšou integrovaná funkcia
v závislosti od súradníc a času. Nazýva sa to vlnová funkcia. V konkrétnom prípade voľného pohybu častice sa vlnová funkcia transformuje na rovinnú de Broglieho vlnu (1). Samotná vlnová funkcia je zavedená ako nejaký pomocný symbol a nepatrí do počtu priamo pozorovateľných veličín. Znalosť toho však umožňuje štatisticky predpovedať hodnoty veličín, ktoré sa získavajú experimentálne, a preto majú skutočný fyzikálny význam.Vlnová funkcia sa používa na určenie relatívnej pravdepodobnosti detekcie častice v rôzne lokality priestor. V tomto štádiu, keď sa diskutuje len o pomeroch pravdepodobnosti, je vlnová funkcia zásadne určená až do ľubovoľného konštantného faktora. Ak je vo všetkých bodoch priestoru vlnová funkcia vynásobená rovnakým konštantným (všeobecne povedané, komplexným) číslom odlišným od nuly, potom dostaneme novú vlnovú funkciu popisujúcu presne ten istý stav. Nemá zmysel tvrdiť, že Ψ sa rovná nule vo všetkých bodoch priestoru, pretože takáto „vlnová funkcia“ nikdy neumožňuje dospieť k záveru o relatívnej pravdepodobnosti detekcie častice na rôznych miestach vo vesmíre. Ale neistotu v definícii Ψ možno výrazne zúžiť, ak prejdeme od relatívnej k absolútnej pravdepodobnosti. Usporiadajme neurčitý faktor vo funkcii Ψ tak, aby hodnota | Ψ | 2dV udávala absolútnu pravdepodobnosť detekcie častice v prvku objemu priestoru dV. Potom | Ψ | 2 = Ψ * Ψ (Ψ * je komplexná konjugovaná funkcia s Ψ) bude mať význam hustoty pravdepodobnosti, ktorú treba očakávať pri pokuse o detekciu častice v priestore. Navyše, Ψ bude stále určené až do ľubovoľného konštantného komplexného faktora, ktorého modul sa však rovná jednej. Pri takejto definícii musí byť splnená podmienka normalizácie:
(2)kde integrál preberá celý nekonečný priestor. To znamená, že častica bude s istotou detekovaná v celom priestore. Ak integrál | Ψ | 2 prevezmeme za určitý objem V1, vypočítame pravdepodobnosť nájdenia častice v objemovom priestore V1.
Normalizácia (2) nemusí byť možná, ak sa integrál (2) líši. Bude tomu tak napríklad v prípade roviny de Broglieho vlny, kedy je pravdepodobnosť detekcie častice vo všetkých bodoch priestoru rovnaká. Takéto prípady by sa však mali považovať za idealizáciu reálnej situácie, v ktorej častica nejde do nekonečna, ale je nútená byť v obmedzenej oblasti priestoru. Potom normalizácia nie je náročná.
Priamy fyzikálny význam teda nie je spojený so samotnou funkciou Ψ, ale s jej modulom Ψ * Ψ. Prečo sa teda v kvantovej teórii operuje s vlnovými funkciami Ψ a nie priamo s experimentálne pozorovanými veličinami * Ψ? To je nevyhnutné pre interpretáciu vlnových vlastností hmoty – interferencie a difrakcie. Tu je situácia úplne rovnaká ako v akejkoľvek vlnovej teórii. Prijíma (aspoň v lineárnej aproximácii) platnosť princípu superpozície samotných vlnových polí a nie ich intenzít, čím dosahuje zahrnutie javov interferencie a difrakcie vĺn do teórie. Takže v kvantovej mechanike je princíp superpozície vlnových funkcií akceptovaný ako jeden z hlavných postulátov, ktorý spočíva v nasledujúcom.
Zo štatistickej interpretácie de Broglieho vĺn (pozri § a Heisenbergov vzťah neurčitosti (pozri § 215)) vyplynulo, že pohybová rovnica v kvantovej mechanike popisujúca pohyb mikročastíc v rôznych silových poliach by mala byť rovnicou, z ktorej by sa dalo pozorovať by nasledovalo - experimentálne dané vlnové vlastnosti častíc.
Hlavnou rovnicou by mala byť rovnica pre vlnovú funkciu, pretože práve ona, alebo presnejšie množstvo | Ф | 2, určuje pravdepodobnosť, že častica zostane v danom čase t v objeme dV, v oblasti so súradnicami a X+ dx, y + dy,
z a Keďže hľadaná rovnica musí zohľadňovať vlnové vlastnosti častíc, musí byť vlnová rovnica, podobne ako rovnica popisujúca elektromagnetické vlny. Základná rovnica nerelativistická kvantová mechanika sformuloval v roku 1926 E. Schrödinger. Schrödingerova rovnica, podobne ako všetky základné rovnice fyziky (napríklad Newtonove rovnice v klasickej mechanike a Maxwellove rovnice pre elektromagnetické pole), nie je odvodená, ale postulovaná. Správnosť tejto rovnice je potvrdená zhodou s experimentom výsledkov získaných pomocou nej, čo jej zase dáva charakter prírodného zákona. Rovnica
 Schrödinger má formu
Schrödinger má formu
|
Pomyselná jednotka y, z, t) -
Potenciálna funkcia častice v silovom poli, v ktorom sa pohybuje; z, t) - požadovaná vlnová funkcia
Rovnica platí pre akúkoľvek časticu (so spinom rovným 0; pozri § 225), ktorá sa pohybuje nízkou (v porovnaní s rýchlosťou svetla) rýchlosťou, teda rýchlosťou v S Dopĺňa sa o podmienky kladené na vlnovú funkciu: 1) vlnová funkcia musí byť konečná, jednohodnotová a spojitá (pozri § 216);
2) deriváty -, -, -, musí-
dx du
aby sme boli nepretržití; 3) funkcia | Ф | 2 musí byť integrovateľná; v najjednoduchších prípadoch sa tento stav redukuje na
Normalizačná podmienka (216,3).
Aby sme dospeli k Schrödingerovej rovnici, uvažujme voľne sa pohybujúcu časticu, ktorá je podľa de Broglieho asociovaná. Pre jednoduchosť uvažujme jednorozmerný prípad. Rovnica rovinnej vlny šíriacej sa pozdĺž osi X, má formu (pozri § 154) t) = A cos - alebo v zložitom zápise t) - V dôsledku toho má de Broglieho rovinná vlna tvar
![]() (217.2)
(217.2)
(berie sa do úvahy, že - = -). V kvantovej th
Exponent sa berie so znamienkom „-“, pretože iba | Ф | 2 má fyzický význam, je to nepodstatné. Potom
 |
Použitie vzťahu medzi energiou E a hybnosť = -) a dosadzovanie
![]() výraz (217.3), dostaneme diferenciálnu rovnicu
výraz (217.3), dostaneme diferenciálnu rovnicu
čo sa zhoduje s rovnicou pre prípad U- Oh (uvažovali sme o voľnej častici).
Ak sa častica pohybuje v silovom poli charakterizovanom potenciálnou energiou u, potom celková energia E pozostáva z kinetickej a potenciálnej energie. Vykonávanie podobného uvažovania a používanie vzťahu medzi („pre
Prípad = EÚ), dospejeme k diferenciálnej rovnici, ktorá sa zhoduje s (217.1).
Vyššie uvedená úvaha by sa nemalo brať ako odvodenie Schrödingerovej rovnice. Vysvetľujú len, ako môžete dospieť k tejto rovnici. Dôkazom správnosti Schrödingerovej rovnice je zhoda so skúsenosťami so závermi, ku ktorým vedie.
Rovnica (217.1) je všeobecná Schrödingerova rovnica. Hovorí sa tomu aj časovo závislou Schrödingerovou rovnicou. Pre mnohé fyzikálne javy vyskytujúce sa v mikrosvete možno rovnicu (217.1) zjednodušiť odstránením časovej závislosti, inými slovami, nájsť Schrödingerovu rovnicu pre stacionárne stavy- stavy s pevnými energetickými hodnotami. Je to možné, ak je silové pole, v ktorom sa častica pohybuje, stacionárne, teda funkcia U = z) nie je vyslovene závislá od času a má význam potenciálnej energie.
V tomto prípade môže byť riešenie Schrödingerovej rovnice reprezentované ako súčin dvoch funkcií, z ktorých jedna je funkciou iba súradníc, druhá iba času a časová závislosť je
Je zjedený faktorom e "= e, takže
![]() (217.4)
(217.4)
kde E je celková energia častice, ktorá je v prípade stacionárneho poľa konštantná. Dosadením (217.4) do (217.1) dostaneme

Odkiaľ, po vydelení spoločným faktorom e zodpovedajúcich transformácií
 Definíciou sa dostávame k rovnici definujúcej funkciu
Definíciou sa dostávame k rovnici definujúcej funkciu
Rovnica urav-
Schrödingerova rovnica pre stacionárne stavy. Táto rovnica obsahuje celkovú energiu ako parameter Ečastice. V teórii diferenciálnych rovníc je dokázané, že takéto rovnice majú nekonečnú množinu riešení, z ktorých cez kladenie okrajových podmienok vybrať riešenia, ktoré majú fyzikálnu
Pre Schrödingerovu rovnicu také podmienky sú podmienky pre pravidelnosť vlnových funkcií: vlnové funkcie musia byť konečné, jednohodnotové a spojité spolu s ich prvými deriváciami.
Skutočný fyzikálny význam teda majú len také riešenia, ktoré sú vyjadrené regulárnymi funkciami. Ale regulárne riešenia sa nevyskytujú pre žiadne hodnoty parametra E, ale len s určitým ich súborom, typickým pre danú úlohu. Títo energetické hodnoty sa volajú vlastné. Riešenia, ktoré zodpovedajú vlastným hodnotám energie, sa nazývajú vlastné funkcie. Vlastné hodnoty E môžu tvoriť spojité aj diskrétne série. V prvom prípade hovoria o nepretržitý, alebo spojité, spektrum, v druhom - asi diskrétne spektrum.
§ 218. Princíp kauzality v kvantovej mechanike
Zo vzťahu neurčitosti sa často usudzuje, že je nepoužiteľný.
princíp kauzality k javom vyskytujúcim sa v mikrokozme. V tomto prípade sú založené na nasledujúcich úvahách. V klasickej mechanike sa podľa princíp kauzality - princíp klasického determinizmu, na známy stav systému v určitom časovom okamihu (úplne určený hodnotami súradníc a hybnosti všetkých častíc systému) a silami, ktoré naň pôsobia, je možné úplne presne nastaviť jeho stav v ktoromkoľvek nasledujúcom okamihu . V dôsledku toho je klasická fyzika založená na nasledujúcom chápaní kauzality: stav mechanického systému v počiatočnom okamihu so známym zákonom o interakcii častíc je príčinou a jeho momentálny stav je dôsledkom.
Na druhej strane, mikroobjekty nemôžu mať súčasne určitú súradnicu a určitú zodpovedajúcu projekciu hybnosti [sú dané vzťahom neurčitosti; preto sa usudzuje, že v počiatočnom okamihu nie je stav systému presne určený. Ak stav systému nie je v počiatočnom okamihu definitívny, nemožno predpovedať nasledujúce stavy, to znamená, že je porušený princíp kauzality.
Nie je však pozorované žiadne porušenie princípu kauzality aplikovaného na mikroobjekty, keďže v kvantovej mechanike nadobúda pojem stav mikroobjektu úplne iný význam ako v klasickej mechanike. V kvantovej mechanike je stav mikroobjektu úplne určený vlnovou funkciou, ktorej druhá mocnina modulu
2 špecifikuje hustotu pravdepodobnosti nájdenia častice v bode so súradnicami x, y, z.
Vlnová funkcia zasa spĺňa rovnicu
Schrödinger obsahujúci prvú časovú deriváciu funkcie Φ. To tiež znamená, že priradenie funkcie (na okamih určuje jej hodnotu v nasledujúcich momentoch. V kvantovej mechanike je teda počiatočný stav príčinou a stav Ф v nasledujúcom momente je dôsledkom. forma principiálnej kauzality v kvantovej mechanike, to znamená, že špecifikácia funkcie predurčuje jej hodnoty pre akékoľvek nasledujúce momenty Stav systému mikročastíc, definovaný v kvantovej mechanike, teda jednoznačne vyplýva z predchádzajúceho stavu, ako to vyžaduje zákon. princíp kauzality...
§ 219. Voľný pohyb častíc
Voľná častica - častica pohybujúca sa v neprítomnosti vonkajších polí. Keďže je voľný (nech sa pohybuje pozdĺž osi X) sily nepôsobia, potom potenciálna energia častice U (x) = const a možno ho považovať za rovný nule. Potom sa celková energia častice zhoduje s jej kinetickou energiou. V tomto prípade má Schrödingerova rovnica (217.5) pre stacionárne stavy tvar
![]() (219.1)
(219.1)
Priamou substitúciou sa môžeme uistiť, že konkrétne riešenie rovnice (219.1) je funkciou - kde A = konšt a Komu= const, s vlastný význam energie
Funkcia = = predstavuje iba súradnicovú časť vlnovej funkcie. Preto časovo závislá vlnová funkcia podľa (217.4),

(219,3) je rovinná monochromatická de Broglieho vlna [viď. (217,2)].
Od výrazu (219.2) vyplýva, že závislosť energie od hybnosti
![]()
sa ukázalo byť bežné pre nerelativistické častice. V dôsledku toho môže voľná častica odoberať energiu akékoľvek hodnoty(od vlnového čísla Komu môže nadobudnúť akékoľvek kladné hodnoty), teda energiu rozsah voľná častica je nepretržitý.
Voľná kvantová častica je teda opísaná rovinnou monochromatickou de Broglieho vlnou. To zodpovedá hustote pravdepodobnosti detekcie častice v danom bode priestoru na čase
to znamená, že všetky polohy voľnej častice v priestore sú ekvipravdepodobné.
§ 220. Častica v jednorozmernej pravouhlej „potenciálnej studni“ s nekonečne vysokým
"steny"
Budeme realizovať kvalitatívna analýza riešenia Schrödingerovej rovnice
 Ryža. 299
Ryža. 299
 (220.4)
(220.4)
špecifické pre časticu v jednorozmerná obdĺžniková „potenciálna studňa“ s nekonečne vysokými „stenami“. Takáto „studňa“ je opísaná potenciálnou energiou formy (pre jednoduchosť predpokladáme, že častica sa pohybuje pozdĺž osi X)

kde je šírka "jamy", a energia sa meria z jeho dna (obr. 299).
Schrödingerovu rovnicu (217.5) pre stacionárne stavy v prípade jednorozmernej úlohy možno zapísať v tvare
![]()
![]() Podľa stavu problému (nekonečne vysoké „steny“) častica neprenikne za „studňu“, preto je pravdepodobnosť jej detekcie (a následne aj vlnovej funkcie) mimo „studne“ rovná nule. . Na hraniciach „jamy“ (at X- 0 a x = funkcia spojitej vlny musí tiež zmiznúť. V dôsledku toho majú okrajové podmienky v tomto prípade tvar
Podľa stavu problému (nekonečne vysoké „steny“) častica neprenikne za „studňu“, preto je pravdepodobnosť jej detekcie (a následne aj vlnovej funkcie) mimo „studne“ rovná nule. . Na hraniciach „jamy“ (at X- 0 a x = funkcia spojitej vlny musí tiež zmiznúť. V dôsledku toho majú okrajové podmienky v tomto prípade tvar
V rámci „jamy“ (0 X Schrödingerova rovnica (220.1) sa redukuje na rovnicu
| |
|||
Všeobecné riešenie diferenciálnej rovnice (220.3):
Keďže podľa (220,2) = 0, potom V= 0.
![]() (220.5)
(220.5)
Stav (220.2) = 0 sa vykoná len pre kde P- celé čísla, to znamená, že je potrebné, aby
 Z výrazov (220.4) a (220.6) vyplýva, že
Z výrazov (220.4) a (220.6) vyplýva, že
to znamená, že stacionárna Schrödingerova rovnica popisujúca pohyb častice v „potenciálnej studni“ s nekonečne vysokými „stenami“ je splnená iba pre vlastné hodnoty závislé od celého čísla. P. Preto energia častice v
"Potenciálna studňa" s nekonečne vysokými "stenami" akceptuje iba určité diskrétne hodnoty, tie. je kvantovaný.
Kvantované energetické hodnoty sa nazývajú energetická hladina, a číslo P, stanovenie energetických hladín častice sa nazýva hlavné kvantové číslo. Mikročastica v „potenciálnej studni“ s nekonečne vysokými „stenami“ teda môže byť len na určitej energetickej úrovni, alebo, ako sa hovorí, častica je v kvante.
Nahradením hodnoty (220,5). Komu z (220.6), nájdeme naše vlastné funkcie:
| |
Integračná konštanta A zistíme z normalizačnej podmienky (216.3), ktorá pre tento prípad môže byť zapísaná vo forme

V výsledok integrácie polo-
A - a budú vyzerať vlastné funkcie

I pomery vlastných funkcií (220,8) zodpovedajúce hladinám
energie (220,7) at n = 1,2, 3 sú znázornené na obr. 300, a. Na obr. 300, b znázorňuje hustotu pravdepodobnosti detekcie častice v rôznych vzdialenostiach od "steny" jamky, ktorá sa rovná =
Pre n = 1, 2 a 3. Z obrázku vyplýva, že napríklad v kvantovom stave s P= 2 častica nemôže byť v strede „jamy“, pričom rovnako často môže byť v jej ľavej a pravej časti. Toto správanie častice naznačuje, že koncepcia trajektórií častíc v kvantovej mechanike je nekonzistentná. Z výrazu (220.7) vyplýva, že energetický interval medzi dvoma
Priľahlé úrovne je
 |
Napríklad pre elektrón s veľkosťou jamky - 10 "1 m (bezplatná el

Kovové tróny) 10 J
To znamená, že energetické hladiny sú umiestnené tak blízko, že spektrum možno prakticky považovať za spojité. Ak sú rozmery jamky úmerné atómovému m), potom J eV pre elektrón, t.j. sa získajú explicitne diskrétne energetické hodnoty (čiarové spektrum).
Teda aplikácia Schrödingerovej rovnice na časticu v „potenciálnej studni“ s nekonečne vysokým
„Steny“ vedú ku kvantovaným energetickým hodnotám, zatiaľ čo klasická mechanika neukladá žiadne obmedzenia na energiu tejto častice.
navyše
Zváženie tohto problému vedie k záveru, že častica „v potenciálovej studni“ s nekonečne vysokým steny„Nemôžem mať menej energie
Minimum, ktoré sa rovná [pozri. (220,7)].
Prítomnosť nenulovej minimálnej energie nie je náhodná a vyplýva zo vzťahu neurčitosti. Neistota súradníc Ohčastice v "jame" so šírkou Ach = Potom podľa vzťahu neistoty impulz nemôže mať presnú, v tomto prípade nulovú hodnotu. Neistota hybnosti
Taký rozsah hodnôt
hybnosť zodpovedá kinetickej energii
![]()
Všetky ostatné úrovne (n > 1) majú energiu presahujúcu túto minimálnu hodnotu.
Od vzorcov (220.9) a (220.7) vyplýva, že pre veľké kvantové čísla
to znamená, že susedné úrovne sú umiestnené blízko: čím bližšie, tým viac P. Ak P je veľmi veľká, potom môžeme hovoriť o takmer nepretržitom slede úrovní a charakteristická vlastnosť kvantových procesov - diskrétnosť - je vyhladená. Tento výsledok je špeciálny prípad princíp Bohrovej korešpondencie (1923), podľa ktorého by zákony kvantovej mechaniky mali pri veľké hodnoty kvantové čísla prechádzajú do zákonov klasickej fyziky.
Viac všeobecný výklad princípu zhody: každá nová, všeobecnejšia teória, ktorá je rozvinutím klasickej, ju úplne nezavrhuje, ale zahŕňa klasickú teóriu s uvedením hraníc jej aplikácie a v určitých obmedzujúcich prípadoch nová teória prechádza do starej. Vzorce pre kinematiku a dynamiku špeciálnej teórie relativity teda prechádzajú na v s vo vzorcoch newtonovskej mechaniky. Napríklad, hoci da Broglieho hypotéza pripisuje vlnové vlastnosti všetkým telesám, v tých prípadoch, keď sa zaoberáme makroskopickými telesami, ich vlnové vlastnosti možno zanedbať; použiť klasickú newtonovskú mechaniku.
§ 221. Prechod častice cez potenciálnu bariéru.
Tunelový efekt
 najjednoduchšiu potenciálovú bariéru pravouhlého tvaru (obr. pre jednorozmerné (po osi pohybu častíc. Pre potenciálovú bariéru pravouhlého tvaru s výškou šírky / môžeme písať
najjednoduchšiu potenciálovú bariéru pravouhlého tvaru (obr. pre jednorozmerné (po osi pohybu častíc. Pre potenciálovú bariéru pravouhlého tvaru s výškou šírky / môžeme písať
Za daných podmienok úlohy klasická častica s energiou E, alebo voľne prejsť cez bariéru (at E> U), alebo sa od nej odrazí (at E< U) sa presunie do opačná strana, t.j. nemôže preniknúť cez bariéru. Pre mikročasticu aj s E> U, existuje nenulová pravdepodobnosť, že častica sa odrazí od bariéry a pohne sa opačným smerom. o E existuje tiež nenulová pravdepodobnosť, že častica bude v oblasti x> tie. prenikne cez bariéru. Takéto zdanlivo paradoxné závery vyplývajú priamo z opísaného riešenia Schrödingerovej rovnice
 412
412
stekanie pohybom mikročastice za podmienok daného problému.
 Rovnica (217.5) pre stacionárne stavy pre každý zo zvýraznených na obr. 301, a región má
Rovnica (217.5) pre stacionárne stavy pre každý zo zvýraznených na obr. 301, a región má
(pre oblasti
(pre oblasť
Všeobecné riešenia tieto diferenciálne rovnice:
Riešenie (221.3) obsahuje aj vlny (po vynásobení časovým faktorom) šíriace sa oboma smermi. Avšak v oblasti 3 existuje len vlna, ktorá prešla cez bariéru a šíri sa zľava doprava. Preto by sa koeficient vo vzorci (221.3) mal brať ako rovný nule.
V oblasti 2
rozhodnutie závisí od vzťahu E> U alebo E
(pre oblasť
(pre oblasť 2);
Význam q a 0, získame riešenia Schrödingerovej rovnice pre tri oblasti v nasledujúcom tvare:
(pre oblasť 3).
V konkrétne pre región 1 celková vlnová funkcia podľa (217.4) bude mať tvar
 |
V tomto výraze je prvým členom rovinná vlna typu (219.3) šíriaca sa v kladnom smere osi X(zodpovedá častici pohybujúcej sa smerom k bariére) a druhá - vlne šíriacej sa v opačnom smere, tj odrazenej od bariéry (zodpovedá častici pohybujúcej sa od bariéry doľava).
(pre oblasť 3).
 V oblasti 2
funkcia už nezodpovedá rovinným vlnám šíreným oboma smermi, keďže exponenty nie sú imaginárne, ale reálne. Dá sa ukázať, že pre konkrétny prípad vysokej a širokej bariéry, keď 1,
V oblasti 2
funkcia už nezodpovedá rovinným vlnám šíreným oboma smermi, keďže exponenty nie sú imaginárne, ale reálne. Dá sa ukázať, že pre konkrétny prípad vysokej a širokej bariéry, keď 1,
Kvalitatívna povaha funkcií je znázornená na obr. 301, z čoho vyplýva, že vlna
Funkcia sa nerovná nule ani vo vnútri bariéry, ale v regióne 3, ak bariéra nie je príliš široká, bude mať opäť formu de Broglieho vĺn s rovnakou hybnosťou, tj s rovnakou frekvenciou, ale s nižšou amplitúdou. Následne sme zistili, že častica má nenulovú pravdepodobnosť, že prejde cez potenciálnu bariéru konečnej šírky.
Kvantová mechanika teda vedie k zásadne novému špecifickému kvantovému javu, ktorý dostal názov tunelový efekt, v dôsledku čoho môže mikroobjekt „prejsť“ cez potenciálnu bariéru. cez spoločné riešenie rovníc pre pravouhlú potenciálovú bariéru dáva (za predpokladu, že koeficient priehľadnosti je malý v porovnaní s jednotkou)
kde je konštantný faktor, ktorý možno prirovnať k jednému; U - potenciálna výška bariéry; E - energia častíc; je šírka bariéry.
Z výrazu (221.7) vyplýva, že D vysoko závislé od hmotnosti Tčastice, šírka / bariéra a od (U -čím je bariéra širšia, tým je menej pravdepodobné, že cez ňu častica prejde.
Pre potenciálnu bariéru ľubovoľného tvaru (obr. 302), spĺňajúcu podmienky tzv poloklasická aproximácia(dostatočne hladký tvar krivky), máme
| |
kde U = U (x).
Z klasického hľadiska je prechod častice cez potenciálnu bariéru pri E nemožné, pretože častica, ktorá sa nachádza v oblasti bariéry, by musela mať zápornú kinetickú energiu. Tunelový efekt je špecifický kvantový efekt.
Prechod častice cez oblasť, do ktorej podľa zákonov klasickej mechaniky nemôže preniknúť, možno vysvetliť vzťahom neurčitosti. Neistota hybnosti Ar na segmente Ach = je Ap> -. Súvisí s týmto rozptylom hodnôt kinetiky hybnosti
 302
302
Česká energetika môže byť
postačujúce na úplné
energia častíc sa ukázala byť vyššia ako potenciálna.
Základy teórie tunelových križovatiek boli položené v prácach L. I. Mandel'shtama
Tunelovanie cez potenciálnu bariéru je základom mnohých javov fyziky pevných látok (napríklad javy v kontaktnej vrstve na rozhraní dvoch polovodičov), atómovej a jadrovej fyziky (napríklad rozpad, termonukleárne reakcie).
§ 222. Lineárny harmonický oscilátor
V kvantovej mechanike
Lineárny harmonický oscilátor- systém v jednorozmernom pohybe pri pôsobení kvázi-elastickej sily je model používaný v mnohých problémoch klasickej a kvantovej teórie (pozri § 142). Príklady klasických harmonických oscilátorov sú pružinové, fyzikálne a matematické kyvadla.
Potenciálna energia harmonického oscilátora [por. (141,5)] sa rovná
Kde je vlastná frekvencia oscilátora; T - hmotnosť častíc.
Závislosť (222.1) má tvar paraboly (obr. 303), tj. „Potenciálna diera“ je v tomto prípade parabolická.
Amplitúda malých kmitov klasického oscilátora je určená jeho celkovou energiou E(pozri obr. 17).
dinger, berúc do úvahy výraz (222.1) pre potenciálnu energiu. Potom sú stacionárne stavy kvantového oscilátora určené Schrödingerovou rovnicou tvaru
![]() = 0, (222.2)
= 0, (222.2)
kde E - celková energia oscilátora. V teórii diferenciálnych rovníc
Je dokázané, že rovnicu (222.2) možno vyriešiť iba pre vlastné hodnoty energie
![]() (222.3)
(222.3)
Vzorec (222.3) ukazuje, že energia kvantového oscilátora môže
mať len diskrétne hodnoty, t.j. je kvantovaný. Energia je obmedzená zdola na nenulovú hodnotu, ako v prípade pravouhlej „studne“ s nekonečne vysokými „stenami“ (pozri § 220), minimálnou hodnotou energie. = Su-
minimálna energia – je to tzv energia nulových vibrácií - je typický pre kvantové systémy a je priamym dôsledkom vzťahu neurčitosti.
Prítomnosť vibrácií nulového bodu znamená, že častica nemôže byť na dne „potenciálnej studne“ (bez ohľadu na tvar studne). „Pád na dno vrtu“ je totiž spojený s vymiznutím hybnosti častice a zároveň s jej neistotou. Potom sa neistota súradnice stane ľubovoľne veľkou, čo je v rozpore s prítomnosťou častice v
"Potenciálna jama".
Záver o prítomnosti energie vibrácií nulového bodu kvantového oscilátora je v rozpore so závermi klasickej teórie, podľa ktorej najmenšia energia, ktorú môže oscilátor mať, je nulová (zodpovedá častici v pokoji v rovnovážnej polohe) . Napríklad podľa záverov klasickej fyziky at T= 0, energia vibračného pohybu atómov kryštálu by mala zaniknúť. V dôsledku toho by mal zmiznúť aj rozptyl svetla v dôsledku vibrácií atómov. Experiment však ukazuje, že intenzita rozptylu svetla s klesajúcou teplotou nie je nulová, ale má tendenciu k určitej limitnej hodnote, čo naznačuje, že pri T 0 vibrácií atómov v kryštáli sa nezastaví. Toto je potvrdenie prítomnosti nulových výkyvov.

Zo vzorca (222.3) tiež vyplýva, že energetické hladiny lineárneho harmonického oscilátora sú umiestnené v rovnakých vzdialenostiach od seba (pozri obr. 303), konkrétne vzdialenosť medzi susednými energetickými hladinami sa rovná minimálnej energetickej hodnote. =
Dôsledné riešenie problému kvantového oscilátora vedie k ďalšiemu významnému rozdielu od klasického
Podľa medzi fyzikmi tak rozšírenej ľudovej slovesnosti sa to stalo takto: v roku 1926 na vedeckom seminári na univerzite v Zürichu vystúpil menovaný teoretický fyzik. Hovoril o zvláštnych nových myšlienkach vznášajúcich sa vo vzduchu, že predmety v mikrokozme sa často správajú viac ako vlny než ako častice. Potom sa o slovo prihlásil starší učiteľ a povedal: „Schrödinger, nevidíš, že je to všetko nezmysel? Alebo všetci nevieme, že vlny - sú to vlny, aby sa dali opísať vlnovými rovnicami? Schrödinger to zobral ako osobnú sťažnosť a rozhodol sa vyvinúť vlnovú rovnicu na opis častíc v rámci kvantovej mechaniky – a s touto úlohou sa vyrovnal bravúrne.
Tu je potrebné uviesť vysvetlenie. V našom každodennom svete sa energia prenáša dvoma spôsobmi: hmotou, keď sa pohybuje z miesta na miesto (napríklad pohybujúcou sa lokomotívou alebo vetrom) - na tomto prenose energie sa podieľajú častice - alebo vlnami (napr. rádiové vlny, ktoré sú vysielané výkonnými vysielačmi a zachytávané anténami našich televízorov). To znamená, že v makrokozme, kde žijeme vy a ja, sú všetci nositelia energie striktne rozdelení na dva typy - korpuskulárne (pozostávajúce z hmotných častíc) alebo vlnové. Každá vlna je navyše opísaná špeciálnym typom rovníc - vlnovými rovnicami. Bez výnimky sú všetky vlny – oceánske vlny, seizmické vlny hornín, rádiové vlny zo vzdialených galaxií – opísané rovnakým typom vlnových rovníc. Toto vysvetlenie je potrebné preto, aby bolo jasné, že ak chceme javy subatomárneho sveta znázorniť z hľadiska vĺn rozdelenia pravdepodobnosti (pozri Kvantová mechanika), musia byť tieto vlny popísané aj príslušnou vlnovou rovnicou.
Schrödinger aplikoval klasickú diferenciálnu rovnicu vlnovej funkcie na koncept pravdepodobnostných vĺn a získal slávnu rovnicu, ktorá nesie jeho meno. Tak ako obvyklá rovnica vlnovej funkcie popisuje šírenie napríklad vlnenia po hladine vody, Schrödingerova rovnica popisuje šírenie vlny pravdepodobnosti nájdenia častice v danom bode priestoru. Vrcholy tejto vlny (body maximálnej pravdepodobnosti) ukazujú, kde sa častica s najväčšou pravdepodobnosťou nachádza vo vesmíre. Hoci Schrödingerova rovnica patrí do oblasti vyššej matematiky, pre pochopenie modernej fyziky je natoľko dôležitá, že ju tu predsa len uvediem – v jej najjednoduchšej forme (tzv. „jednorozmerná stacionárna Schrödingerova rovnica“). Vyššie uvedená vlnová funkcia rozdelenia pravdepodobnosti, označená gréckym písmenom ("psi"), je riešením nasledujúcej diferenciálnej rovnice (je v poriadku, ak jej nerozumiete; hlavnou vecou je veriť, že táto rovnica naznačuje, že pravdepodobnosť sa správa ako vlna):
Obraz kvantových dejov, ktorý nám dáva Schrödingerova rovnica, je taký, že elektróny a iné elementárne častice sa na hladine oceánu správajú ako vlny. V priebehu času sa vrchol vlny (zodpovedajúci miestu, kde sa s najväčšou pravdepodobnosťou nachádza elektrón) posúva v priestore v súlade s rovnicou popisujúcou túto vlnu. To znamená, že to, čo sme tradične považovali za časticu v kvantovom svete, sa správa podobne ako vlna.
Keď Schrödinger prvýkrát zverejnil svoje výsledky, vo svete teoretickej fyziky vypukla búrka v šálke. Faktom je, že prakticky v rovnakom čase sa objavilo dielo Schrödingerovho súčasníka Wernera Heisenberga (pozri Heisenbergov princíp neurčitosti), v ktorom autor predložil koncept „maticovej mechaniky“, kde sa riešia rovnaké problémy kvantovej mechaniky. boli riešené inou, z matematického hľadiska zložitejšou v maticovej forme. Rozruch vyvolalo to, že vedci sa jednoducho báli, že dva rovnako presvedčivé prístupy k popisu mikrosveta si protirečia. Nadšenie bolo márne. Sám Schrödinger v tom istom roku dokázal úplnú ekvivalenciu oboch teórií – teda maticová rovnica vyplýva z vlnovej rovnice a naopak; výsledky sú totožné. Dnes sa používa väčšina Schrödingerovej verzie (niekedy sa jeho teória nazýva „vlnová mechanika“), pretože jeho rovnica je menej ťažkopádna a ľahšie sa učí.
Nie je však také ľahké predstaviť si a prijať, že niečo ako elektrón sa správa ako vlna. V každodennom živote sa stretávame buď s časticou alebo vlnou. Lopta je častica, zvuk je vlna a to je všetko. Vo svete kvantovej mechaniky veci nie sú také jednoduché. V skutočnosti – a experimenty to čoskoro ukázali – v kvantovom svete sa entity líšia od objektov, na ktoré sme zvyknutí, a majú iné vlastnosti. Svetlo, ktoré sme považovali za vlnu, sa niekedy správa ako častica (nazývaná fotón) a častice ako elektrón a protón sa môžu správať ako vlny (pozri Princíp komplementarity).
Tento problém sa zvyčajne nazýva duálna alebo dvojitá vlnovo-časticová povaha kvantových častíc a je zjavne inherentná všetkým objektom subatomárneho sveta (pozri Bellovu vetu). Musíme pochopiť, že v mikrokozme sú naše každodenné intuitívne predstavy o tom, aké formy môže mať hmota a ako sa môže správať, jednoducho nepoužiteľné. Samotný fakt, že používame vlnovú rovnicu na opis pohybu toho, čo sme považovali za častice, je toho jasným dôkazom. Ako je uvedené v úvode, nie je v tom žiadny zvláštny rozpor. Koniec koncov, nemáme žiadny presvedčivý dôvod domnievať sa, že to, čo pozorujeme v makrokozme, by sa malo presne reprodukovať na úrovni mikrokozmu. Napriek tomu duálna povaha elementárnych častíc zostáva pre mnohých ľudí jedným z najviac nepochopiteľných a znepokojujúcich aspektov kvantovej mechaniky a nebolo by prehnané povedať, že všetky problémy začali Erwinom Schrödingerom.
Encyklopédia Jamesa Trefila The Nature of Science. 200 zákonov vesmíru“.
James Trefil je profesor fyziky na George Mason University (USA), jeden z najznámejších západných autorov populárno-vedeckých kníh.
| Komentáre: 0 |
Max Planck, jeden zo zakladateľov kvantovej mechaniky, prišiel na myšlienku kvantovania energie, pričom sa pokúsil teoreticky vysvetliť proces interakcie medzi nedávno objavenými elektromagnetickými vlnami a atómami, a tým vyriešiť problém žiarenia čierneho telesa. Uvedomil si, že na vysvetlenie pozorovaného emisného spektra atómov je potrebné brať za samozrejmosť, že atómy vyžarujú a absorbujú energiu po častiach (ktoré vedec nazval kvantá) a iba pri samostatných vlnových frekvenciách.
Absolútne čierne teleso, ktoré úplne pohltí elektromagnetické žiarenie akejkoľvek frekvencie, pri zahriatí vyžaruje energiu vo forme vĺn rovnomerne rozložených v celom frekvenčnom spektre.
Slovo „quantum“ pochádza z latinského quantum („koľko, koľko“) a anglického quantum („množstvo, porcia, kvantum“). Oddávna je zvykom nazývať vedu o pohybe hmoty „mechanika“. V súlade s tým výraz „kvantová mechanika“ znamená vedu o pohybe hmoty po častiach (alebo v modernom vedeckom jazyku vedu o pohybe kvantovania hmoty). Termín „kvantový“ zaviedol nemecký fyzik Max Planck, aby opísal interakciu svetla s atómami.
Jedným z faktov subatomárneho sveta je, že jeho objekty – ako sú elektróny alebo fotóny – sa vôbec nepodobajú bežným objektom makrokozmu. Správajú sa nie ako častice a nie ako vlny, ale ako úplne špeciálne útvary, ktoré v závislosti od okolností vykazujú vlnové aj korpuskulárne vlastnosti. Jedna vec je deklarovať a druhá vec je spojiť vlnové a korpuskulárne aspekty správania kvantových častíc a opísať ich presnou rovnicou. Presne to sa dialo vo vzťahu de Broglie.
V každodennom živote existujú dva spôsoby prenosu energie vo vesmíre – prostredníctvom častíc alebo vĺn. V každodennom živote nie sú medzi týmito dvoma mechanizmami prenosu energie viditeľné rozpory. Takže basketbalová lopta je častica a zvuk je vlna a všetko je jasné. V kvantovej mechanike však veci nie sú také jednoduché. Aj z tých najjednoduchších experimentov s kvantovými objektmi je čoskoro jasné, že nám známe princípy a zákony makrokozmu v mikrokozme nefungujú. Svetlo, ktoré sme zvyknutí chápať ako vlnu, sa niekedy správa tak, ako keby pozostávalo z prúdu častíc (fotónov) a elementárne častice, ako je elektrón alebo dokonca masívny protón, často vykazujú vlastnosti vlny.
Najviac zo všetkého Einstein protestoval proti potrebe opisovať javy mikrosveta z hľadiska pravdepodobností a vlnových funkcií, a nie z bežnej polohy súradníc a rýchlostí častíc. To myslel tým „kocky“. Uvedomil si, že popis pohybu elektrónov z hľadiska ich rýchlostí a súradníc je v rozpore s princípom neurčitosti. Einstein však tvrdil, že musia existovať nejaké ďalšie premenné alebo parametre, berúc do úvahy, s ktorými sa kvantovo-mechanický obraz mikrosveta vráti na cestu integrity a determinizmu. To znamená, tvrdil, len sa nám zdá, že Boh s nami hrá kocky, pretože nerozumieme všetkému. Ako prvý teda sformuloval hypotézu o skrytej premennej v rovniciach kvantovej mechaniky. Spočíva v tom, že elektróny majú v skutočnosti pevné súradnice a rýchlosť ako newtonovské biliardové gule a princíp neurčitosti a pravdepodobnostný prístup k ich určovaniu v rámci kvantovej mechaniky sú výsledkom neúplnosti samotnej teórie, ktorá je prečo im to neumožňuje určité definovať.
Júlia Zotová
Dozviete sa: Aké technológie sa nazývajú kvantové a prečo. Aká je výhoda kvantových technológií oproti klasickým. Čo kvantový počítač môže a čo nemôže. Ako fyzici vyrábajú kvantový počítač. Kedy bude vytvorený.
 Francúzsky fyzik Pierre Simon Laplace nastolil dôležitú otázku, či je všetko na svete predurčené predchádzajúcim stavom sveta, alebo či príčina môže spôsobiť viaceré následky. Ako predpokladá filozofická tradícia, sám Laplace vo svojej knihe „Prezentácia systému sveta“ nekládol žiadne otázky, ale povedal hotovú odpoveď, že áno, všetko na svete je predurčené, no ako často sa deje vo filozofii, Laplaceova predstava sveta nepresvedčila každého, a tak jeho odpoveď vyvolala diskusiu o tejto problematike, ktorá trvá dodnes. Napriek názoru niektorých filozofov, že kvantová mechanika tento problém vyriešila v prospech pravdepodobnostného prístupu, sa o Laplaceovej teórii úplného predurčenia, alebo ako sa inak hovorí, o teórii Laplaceovho determinizmu, diskutuje dodnes.
Francúzsky fyzik Pierre Simon Laplace nastolil dôležitú otázku, či je všetko na svete predurčené predchádzajúcim stavom sveta, alebo či príčina môže spôsobiť viaceré následky. Ako predpokladá filozofická tradícia, sám Laplace vo svojej knihe „Prezentácia systému sveta“ nekládol žiadne otázky, ale povedal hotovú odpoveď, že áno, všetko na svete je predurčené, no ako často sa deje vo filozofii, Laplaceova predstava sveta nepresvedčila každého, a tak jeho odpoveď vyvolala diskusiu o tejto problematike, ktorá trvá dodnes. Napriek názoru niektorých filozofov, že kvantová mechanika tento problém vyriešila v prospech pravdepodobnostného prístupu, sa o Laplaceovej teórii úplného predurčenia, alebo ako sa inak hovorí, o teórii Laplaceovho determinizmu, diskutuje dodnes.
Gordey Lesovik
Pred časom sme so skupinou spoluautorov začali odvodzovať druhý termodynamický zákon z pohľadu kvantovej mechaniky. Napríklad v jednej z jeho formulácií, ktorá hovorí, že entropia uzavretého systému sa neznižuje, typicky sa zvyšuje a niekedy zostáva konštantná, ak je systém energeticky izolovaný. Pomocou dobre známych výsledkov kvantovej teórie informácie sme odvodili niektoré podmienky, za ktorých je toto tvrdenie pravdivé. Neočakávane sa zistilo, že tieto podmienky sa nezhodujú s podmienkou energetickej izolácie systémov.
 Profesor fyziky Jim Al-Khalili skúma najpresnejšiu a jednu z najviac mätúcich teórií vedy – kvantovú fyziku. Začiatkom 20. storočia vedci prenikli do skrytých hlbín hmoty, subatomárnych stavebných kameňov sveta okolo nás. Objavili javy, ktoré sa líšili od všetkého, čo predtým videli. Svet, kde môže byť všetko súčasne na mnohých miestach, kde realita skutočne existuje len vtedy, keď ju pozorujeme. Albert Einstein sa bránil iba myšlienke, že podstata prírody je založená na náhode. Kvantová fyzika naznačuje, že subatomárne častice môžu interagovať rýchlejšie ako rýchlosť svetla, čo je v rozpore s jeho teóriou relativity.
Profesor fyziky Jim Al-Khalili skúma najpresnejšiu a jednu z najviac mätúcich teórií vedy – kvantovú fyziku. Začiatkom 20. storočia vedci prenikli do skrytých hlbín hmoty, subatomárnych stavebných kameňov sveta okolo nás. Objavili javy, ktoré sa líšili od všetkého, čo predtým videli. Svet, kde môže byť všetko súčasne na mnohých miestach, kde realita skutočne existuje len vtedy, keď ju pozorujeme. Albert Einstein sa bránil iba myšlienke, že podstata prírody je založená na náhode. Kvantová fyzika naznačuje, že subatomárne častice môžu interagovať rýchlejšie ako rýchlosť svetla, čo je v rozpore s jeho teóriou relativity.